Tính A:
A=1/51 + 1/52 + 1/53 + ......... + 1/100
Tính A:
A=1/51 + 1/52 + 1/53 + ......... + 1/100
Tính A=1/51+1/52+1/53+...+1/99+1/100
Cho A=1/51+1/52+1/53+...+1/100 và B=1/2+1/12+1/30+...+1/9900.
Tính A-B
Tính nhanh A=1/51+1/52+1/53+...+1/100
GIÚP MIK NHA , AI NHANH MIK TICK CHO
TL
50/3227
Hok tốt nghen
Cho A=1/51+1/52+1/53+...+1/100
Cho B=1/2+1/12+1/30+...+1/9900
Tính A-B
\(A=\dfrac{1}{51}+\dfrac{1}{52}+\dfrac{1}{53}+...+\dfrac{1}{100}\)
Tham khảo: (mk chx chắc lắm đâu nha)
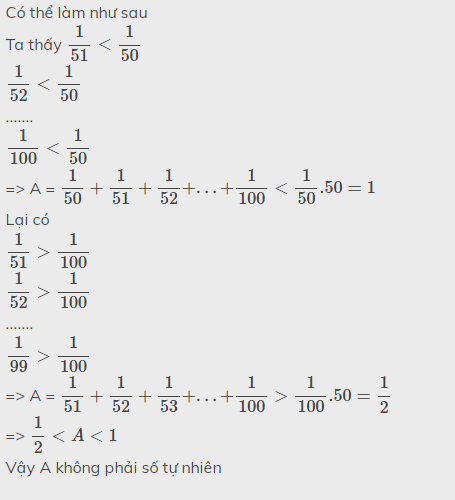
Tính tổng 1/51+1/52+1/53+...+1/99+1/100
Ta có:\(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}=\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-\left(1+\frac{1}{2}+...+\frac{1}{50}\right)=\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-2.\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}\)
@Ác Mộng ở đoạn cuối tự nhiên bỏ mất số 2 luôn, giải sai rồi kìa
a. A=1/51+1/52+1/53+...+1/100; B=1/1.2+1/3.4+...+1/99.100
Chứng tỏ A = 1/51 + 1/52 + 1/53 + .....+1/99 + 1/100 <1/2
Đề sai tại vì:
Ta thấy từ: \(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{99}\) mỗi số hạng đều lớn hơn \(\frac{1}{100}\)
Mà tổng trên có : ( 100 - 51 ) + 1 = 50 ( số hạng )
Nên:
\(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{99}+\frac{1}{100}>\frac{1}{100}.50=\frac{50}{100}=\frac{1}{2}\)
Vậy : \(A>\frac{1}{2}\)