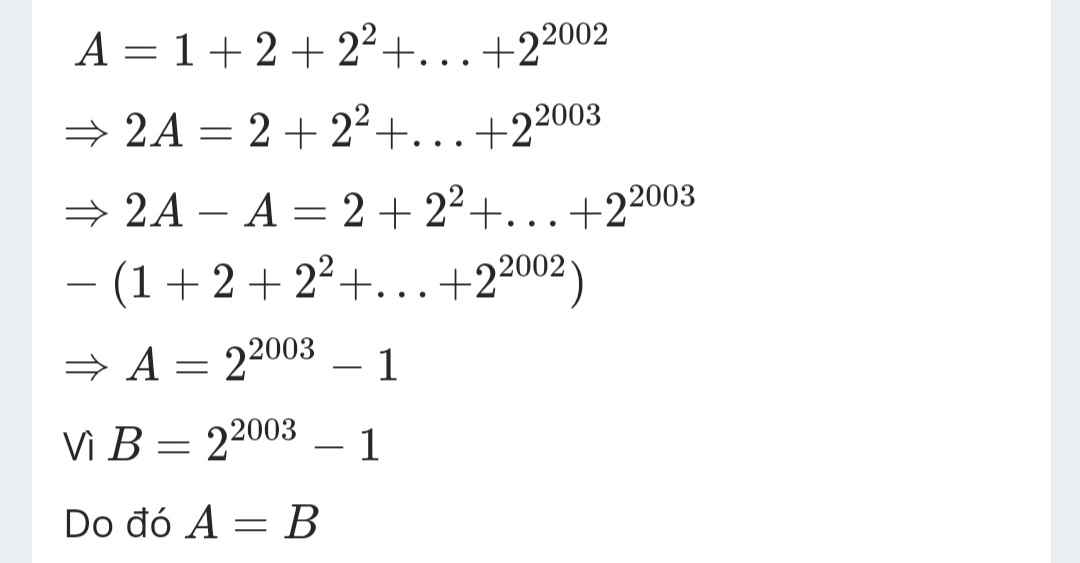Cho A=1+2+2^2+2^3+.......+2^2002 và B=2^2003. So sánh A và B
H24
Những câu hỏi liên quan
Cho A= 1 + 2 + 2^2 + … + 2^2002 và B = 2^2003 – 1. So sánh A và B
\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)
Đúng 0
Bình luận (0)
\(A=1+2+2^2+...+2^{2002}\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+...+2^{2002}\right)\)
\(A=2^{2003}-1\)
⇒ \(A=B\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
2) Cho A = 1 + 2 + 2^2 + 2^3 + 2^4 + ... + 2^2001 + 2^2002 và B = 2^2003. So sánh A và B.
A = 1 + 2 + 2² + ... + 2^2002
A = 1 + (2 + 2² + ... + 2^2002 )
Ta xét :
u1 = 2
u2 = 2.2 = 22
u3 = 2.22 = 2^3
u2002 = 2.2^2001 = 2^2002
Tổng cấp số nhân : S = u1.(1 - q^n) / (1 - q) = 2.(1 - 2^2002) / (1 - 2) = 2(2^2002 - 1) = 2^2003 - 2
A = 1 + 2^2003 - 2 = 2^2003 - 1
So sánh với B
2^2003 - 1 = 2^2003 - 1
Vậy B = A
Đúng 0
Bình luận (0)
=>2A=2+2^2+2^3+2^4+2^5+...+2^2002+2^2003
=>2A-A=2^2003-1
=>A=2^2003-1
=>A<B
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho A = 1+2+2^2+2^3+2^4+.........+2^2002
B = 2^2003
so sánh A và B
Ta có:\(A=1+2+2^2+2^3+...+2^{2002}\)
\(2A=2\left(1+2+2^2+2^3+...+2^{2002}\right)\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-B=\left(2+2^2+2^3+2^4+...+2^{2003}\right)-2^{2003}\)
\(A-1=2+2^2+2^3+...+2^{2002}\)
\(\Rightarrow A-1=2A-B\)
\(\Rightarrow A>B\)
Đúng 0
Bình luận (0)
cho a=1+2+2^2+...+2^2002
Cho b=2^2003-1
so sánh a và b
ta có : a = 1 + 2 + 2^2 + ... + 2^2002
=> 2a = 2 + 2^2 + 2^3 + ... + 2^2003
=> 2a-a = (2+2^2 + 2^3 + ... + 2^2003) - ( 1+2+2^2+...+2^2002)
=> a = 2^2003 - 1
Vậy a=b
Đúng 0
Bình luận (0)
Cho A = 1+2+22 +…+22002 và B = 22003 -1.
So sánh a và b
\(A=1+2+2^2+.....+2^{2002}\)
\(\Rightarrow2A=2+2^2+2^3+......+2^{2003}\)
\(\Rightarrow2A-A=2^{2013}-1=B\)
Đúng 0
Bình luận (0)
So sánh A và B
A=1+2+2^2+......+2^2002
B=2^2003
A = 1 + 2 + 22 + ... + 22002
=> 2A = 2(1 + 2 + 22 + ... + 22002 )
= 2 + 22 + 23 + .... + 22003
2A - A = ( 2 + 22 + 23 + .... + 22003 ) - ( 1 + 2 + 22 + ... + 22002 )
A = 22003 - 1
Vì 22003 - 1 < 22003 nên A < B
Vậy A < B
Đúng 1
Bình luận (0)
Chứng minh ( 12n + 1 , 30n + 1 ) = 1
2 .
So sánh A và B
Cho A = 1 + 2 + 2^2 + ......... + 2^2002 và B = 2^2003
Đặt d=UCLN(12n+1, 30n+1)
Khi đó: \(\hept{\begin{cases}12n+1⋮d\\30n+1⋮d\end{cases}}\)<=> 5(12n+1)-2(30n+1)\(⋮\)d <=> 3\(⋮\)d
Nên d=1 hoặc d=3
Mặt khác: 12n\(⋮\)3=> 12n+1 không chia hết cho 3
do đó d\(\ne\)3
Vậy d=1 (ĐPCM)
Đúng 0
Bình luận (0)
2,
A=\(1+2+2^2+...+2^{2002}\)\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\)
=> \(A=2A-A=2^{2003}-1< B\)
Đúng 0
Bình luận (0)
1/Chứng minh : 5^2003+5^2002+5^2001 chia hết cho 31'
2./ Cho A = 1+2+2^2+......+2^9+2^10 và B = 2^11- 1 .So sánh A B
2/
A=1+2+2^2+...+2^10
2.A= 2+2^2+...+2^11
=>2A-A = 2^11-1=> A = 2^11 -1=B
Vậy A=B
Đúng 0
Bình luận (0)
1)52003+52002+52001=52001(52+5+1)=52001(25+5+1)=52001.31
Vì 31 chia hết cho 31nên
52001.31chia hết cho 31 hay 52003+52002+52001 chia hết cho 31
2) A = 1+2+22+......+29+210
=>2A=2+22+23+...+211
=>2A-A=2+22+23+...+211-(1+2+22+...+29+210)
=>A=211-1
Vậy A=B=211-1
Đúng 0
Bình luận (0)
so sánh hai số biết
a) a=1+3+3^2+3^3+...+3^6 và b=3^7-1
b) c=1+2+2^2+2^3+....+2^2002 và d=2^2003-1
Giai ra chi tiết
a ) Ta có:
A = 1 + 3 + 32 + 33+ ..... + 36
A x 3 = 3 + 32 + 33 + 34 + .... + 37
A x 2 - A = ( 3 + 32 + 33 + 34 + .... + 37 ) - ( 1 + 3 + 32 + 33 + .... + 36 )
A = 37 - 1
Mà : B = 37 - 1 nên A = B
b ) Ta có :
C = 1 + 2 + 22 + 23 + ...... + 22002
C x 2 = 2 + 22 + 23 + 24 + ..... + 22003
C x 2 - C = ( 2 + 22 + 23 + 24 + ...... + 22003 ) - ( 1 + 2 + 22 + 23 + ..... + 22002 )
C = 22003 - 1
Mà : D = 22003 - 1 nên C = D
Đúng 0
Bình luận (0)
A=1+3+3^2+....+3^100
\Rightarrow 3A=3+ +
+...+
\Rightarrow3A-A=2A=(3+ +
+
)-(1+3+
+....+
)
= -1
\RightarrowA=( -1):2
Đúng 0
Bình luận (0)