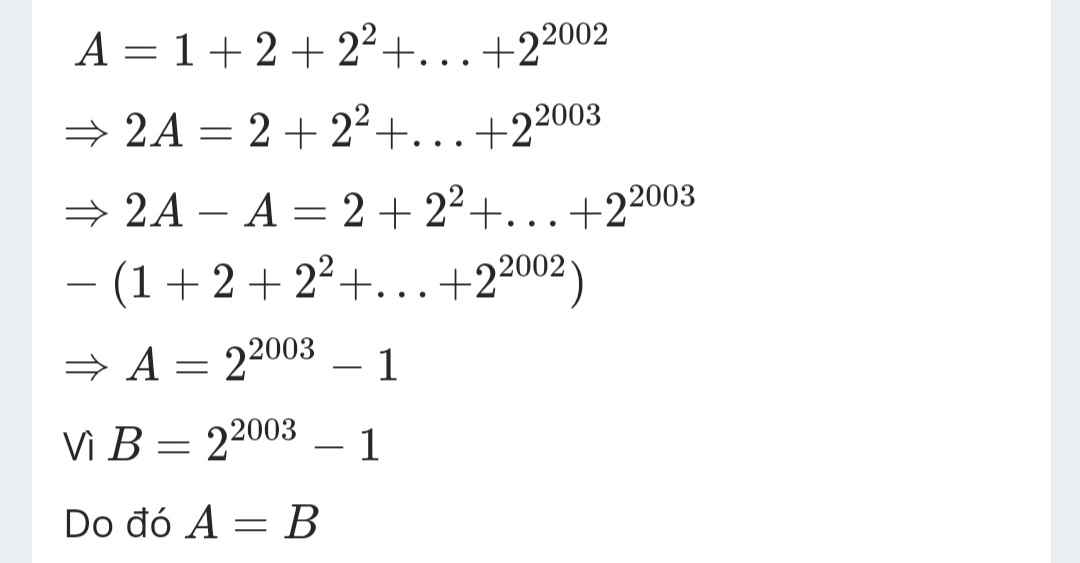\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)
\(A=1+2+2^2+...+2^{2002}\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+...+2^{2002}\right)\)
\(A=2^{2003}-1\)
⇒ \(A=B\)
A=1+2+22+...+22002A=1+2+22+...+22002
2A=2+22+23+...+220032A=2+22+23+...+22003
2A−A=(2+22+23+...+22003)−(1+2+22+...+22002)2A−A=(2+22+23+...+22003)−(1+2+22+...+22002)
A=22003−1A=22003−1
⇒ A=B