Cho ΔABC có AH là đường cao, gọi D và E là hình chiếu của H trên AB,AC. CMinh ΔAED đồng dạng ΔABC
TQ
Những câu hỏi liên quan
Cho ΔABC vuông tại A, đường cao AH. Gọi E,F lầ lượt là hình chiếu của H trên AB và AC a) Chứng minh ΔAFE ∼ ΔABC b) Chứng minh AH^3 BC.BE.CF
Đọc tiếp
Cho ΔABC vuông tại A, đường cao AH. Gọi E,F lầ lượt là hình chiếu của H trên AB và AC a) Chứng minh ΔAFE ∼ ΔABC b) Chứng minh AH^3= BC.BE.CF
Lời giải:
a. Áp dụng HTL trong tam giác vuông ta có:
$AE.AB=AH^2$
$AF.AC=AH^2$
$\Rightarrow AE.AB=AF.AC\Rightarrow \frac{AE}{AF}=\frac{AC}{AB}$
Xét tam giác $AFE$ và $ABC$ có:
$\widehat{EAF}=\widehat{CAB}=90^0$
$\frac{AE}{AF}=\frac{AC}{AB}$ (cmt)
$\Rightarrow \triangle AFE\sim \triangle ABC$ (c.g.c)
b.
Áp dụng HTL trong tam giác vuông:
$BE.BA=BH^2$
$CF.CA=CH^2$
$\Rightarrow BE.CF.AB.AC=(BH.CH)^2=(AH^2)^2$
$\Leftrightarrow BE.CF.2S_{ABC}=AH^4$
$\Leftrightarrow BE.CF.AH.BC=AH^4$
$\Leftrightarrow BE.CF.BC=AH^3$ (đpcm)
Đúng 1
Bình luận (0)
cho ΔABC ⊥ tại A đường cao AH , biết BC = 20 cm AH = 8 cm , lấy E và D là hình chiếu của H trên AB và AC
a, ADHE là hình gì ? chứng minh .
b. chứng minh ΔADE đồng dạng với ΔABC
c, tính diện tích ΔADE
a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HE là đường cao
nên AE*AC=AH^2=AD*AB
=>AE/AB=AD/AC
=>ΔAED đồng dạng với ΔABC
c: ΔAED đồng dạng với ΔABC
=>\(\dfrac{S_{AED}}{S_{ABC}}=\left(\dfrac{ED}{BC}\right)^2=\dfrac{4}{25}\)
=>\(S_{AED}=\dfrac{4}{25}\cdot80=\dfrac{320}{25}=12.8\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
Chứng minh: ∠ADE = ∠BHD
\(\widehat{BHD}=\widehat{HAB}\)
\(\widehat{HAB}=\widehat{ADE}\)
Do đó: \(\widehat{ADE}=\widehat{BHD}\)
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A có AB = 12cm, AC = 16cm và đường cao AH.
a) C/m: ΔHCA đồng dạng ΔACB
b) C/m: AB2=BH.BC
c) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. C/m: AE.AB=AF.AC
a: Xét ΔHCA vuông tại H và ΔACB vuông tại A có
góc HCA chung
Do đó:ΔHCA\(\sim\)ΔACB
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\)
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
XétΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AH. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Tam giác AIK đồng dạng với tam giác nào dưới đây?
A. ACB
B. ABC
C. CAB
D. BAC
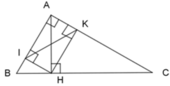
Gọi I, K lần lượt là hình chiếu của H lên AB và AC.
⇒ H I A ^ = H K A ^ = 90 ∘
Xét tứ giác AIHK có: I A K ^ = H I A ^ = H K A ^ = 90 ∘
=> Tứ giác AIHK là hình chữ nhật (dhnb)
+) Xét ΔAIK và ΔIAH ta có:
AI chung
AK = IH (theo tính chất của hình chữ nhật)
AH = IK (theo tính chất của hình chữ nhật)
=> ΔAIK = ΔIAH (c - c - c) (1)
Xét 2 tam giác vuông ΔIAH và ΔHAB có: A chung
=> ΔIAH ~ ΔHAB (g - g) (2)
Xét 2 tam giác vuông ΔHAB và ΔACB có: B chung
=> ΔHAB ~ ΔACB (g - g) (3)
Từ (1), (2) và (3) ta có: ΔAIK ~ ΔACB
Đáp án: A
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A (AB<AC), đường cao AH (H∈BC). BD là phân giác của ∠ABC (D∈AC). Gọi I là giao điểm của AH và BD.
a. Chứng minh: ΔHBA đồng dạng ΔABC và ΔHBI đồng dạng ΔABD
b. Chứng minh: \(\frac{IA}{IH}=\frac{BC}{AB}\)
c. Đường thẳng vuông góc với BD tại B cắt đường thẳng AH tại M. CHứng minh: MA.IH = MH.IA
Giúp mình ý b,c với ạ
Làm giúp mik phần C ạ
Bài 6. Cho ΔABC vuông tại A có AB<AC , đường cao AH và trung tuyến AE. Gọi D, F lần lượt là hình chiếu của E trên AB, AC
a) Chứng minh ΔDBE = ΔFEC và tứ giác BDFE là hình bình hành.
b) Chứng minh F là trung điểm của AC và DFEH là hình thang cân.
c) Lấy M sao cho F là trung điểm của EM và N sao cho F là trung điểm của BN . Chứng minh A, N, M thẳng hàng.
Cho ΔABC vuông tại A, đường cao AH. Gọi D và E thứ tự là hình chiếu của H trên AB và AC. a) Chứng minh: AH=DE b) Chứng minh: AD. AB=AE. AC c) Biết AH=12cm; BH=9cm. Tính diện tích ABC. d) Gọi M là trung điểm của BC. Chứng minh DE vuông góc với AM
a, Xét tứ giác ADHE có :
^A = ^ADH = ^HEA = 900
Vậy tứ giác ADHE là hcn
Vậy AH = DE ( 2 đường chéo bằng nhau )
b, Xét tam giác AEH và tam giác AHC có :
^AEH = ^AHC = 900
^A _ chung
Vậy tam giác AEH ~ tam giác AHC ( g.g )
=> AH/AC = AE/AH => AH^2 = AE.AC (1)
tương tự với tam giác ADH ~ tam giác AHB (g.g)
=> AD/AH = AH/AB => AH^2=AD.AB (2)
Từ (1) ; (2) suy ra AE.AC = AD.AB
c, Xét tam giác ABH và tam giác CAH
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác ABH ~ tam giác CAH (g.g)
=> AH/CH = BH/AH => AH^2 = BH.CH
=> CH = AH^2/BH = 144/9 = 16
=> BC = BH + CH = 25 cm
Diện tích tam giác ABC là : SABC = 1/2 . AH . BC
= 1/2 . 12 . 25 = 150 cm2
Đúng 4
Bình luận (0)
Cho ΔABC nhọn, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.CMR:
a) DE=AH.SinA
b) Cho AI là phân giác góc A, \(\widehat{A}=60^o\). CMR: \(\dfrac{\sqrt{3}}{AI}=\dfrac{1}{AB}+\dfrac{1}{AC}\)
a, Gọi giao điểm của AB và EH là O
Xét tg AEO có \(\sin\widehat{A}=\dfrac{OE}{OA}\)
Vì \(\left\{{}\begin{matrix}\widehat{OEA}=\widehat{HDO}=90^0\\\widehat{AOE}.chung\end{matrix}\right.\) nên \(\Delta ODH\sim\Delta OEA\left(g.g\right)\)
\(\Rightarrow\dfrac{OD}{OE}=\dfrac{OH}{OA}\)
Vì \(\left\{{}\begin{matrix}\dfrac{OD}{OE}=\dfrac{OH}{OA}\\\widehat{AOE}.chung\end{matrix}\right.\) nên \(\Delta OHA\sim\Delta ODE\left(c.g.c\right)\)
\(\Rightarrow\dfrac{DE}{AH}=\dfrac{OE}{OA}=\sin\widehat{A}\\ \Rightarrow DE=AH\cdot\sin\widehat{A}\)
b, Áp dụng công thức diện tích tam giác bằng \(\dfrac{1}{2}\) tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
\(S_{ABC}=S_{AIB}+S_{AIC}\\ \Rightarrow\dfrac{1}{2}\cdot AB\cdot AC\cdot\sin\widehat{BAC}=\dfrac{1}{2}\cdot AB\cdot AI\cdot\sin\widehat{BAI}+\dfrac{1}{2}AC\cdot AI\cdot\sin\widehat{CAI}\)
Mà AI là p/g nên \(\widehat{BAI}=\widehat{CAI}=\dfrac{1}{2}\widehat{BAC}=30^0\)
\(\Rightarrow\dfrac{1}{2}AB\cdot AC\cdot\sin60^0=\dfrac{1}{2}AB\cdot AI\cdot\sin30^0+\dfrac{1}{2}AC\cdot AI\cdot\sin30^0\\ \Rightarrow\dfrac{\sqrt{3}}{4}\cdot AB\cdot AC=\dfrac{1}{4}AB\cdot AI+\dfrac{1}{4}AC\cdot AI\\ \Rightarrow\dfrac{\sqrt{3}}{4}\cdot AB\cdot AC=\dfrac{1}{4}AI\left(AB+AC\right)\\ \Rightarrow\dfrac{\dfrac{\sqrt{3}}{4}}{\dfrac{1}{4}AI}=\dfrac{AB+AC}{AB\cdot AC}\\ \Rightarrow\dfrac{\sqrt{3}}{AI}=\dfrac{1}{AB}+\dfrac{1}{AC}\left(đpcm\right)\)
Đúng 2
Bình luận (2)
Cho ΔABC vuông tại A, đường cao AH. Gọi K và M lần lượt là hình chiếu của H trên AB và AC. Gọi N là trung điểm của CH. Số đo góc ∠KMN là:
A. 30 °
B. 60 °
C. 90 °
D. 120 °