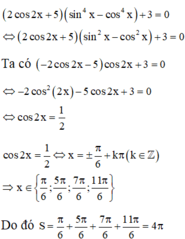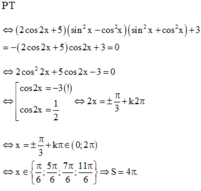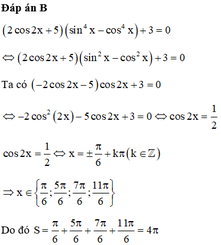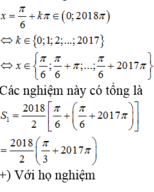Tính tổng S các nghiệm của phương trình (2cos2x+5)(sin4x-cos4x)+3=0 trong khoảng(0;2π)
NV
Những câu hỏi liên quan
Tính tổng S các nghiệm của phương trình (2cos2x+5) (
sin
4
x
-
cos
4
x
)+3 0 trong khoảng
0
;
2
π
A.
S
11
π
6
B. S 4
π
C. S 5
π
D. S ...
Đọc tiếp
Tính tổng S các nghiệm của phương trình (2cos2x+5)
( sin 4 x - cos 4 x )+3 = 0 trong khoảng 0 ; 2 π
A. S = 11 π 6
B. S = 4 π
C. S = 5 π
D. S = 7 π 6
Tính tổng S các nghiệm của phương trình (2cos2x+5) (
sin
4
x
-
cos
4
x
)
+
3
0
trong khoảng
0
;
2
π
Đọc tiếp
Tính tổng S các nghiệm của phương trình (2cos2x+5)
( sin 4 x - cos 4 x ) + 3 = 0 trong khoảng 0 ; 2 π
![]()
![]()
![]()
![]()
Tính tổng S các nghiệm của phương trình
(
2
c
o
s
2
x
+
5
)
(
s
i
n
4
x
-
c
o
s
4
x
)
+
3
0
trong khoảng (0;2018ᴨ) A.
2020
.
2018
π
B.
1010
.
2018
π...
Đọc tiếp
Tính tổng S các nghiệm của phương trình ( 2 c o s 2 x + 5 ) ( s i n 4 x - c o s 4 x ) + 3 = 0 trong khoảng (0;2018ᴨ)
A. 2020 . 2018 π
B. 1010 . 2018 π
C. 2018 . 2018 π
D. 2016 . 2018 π
Tính tổng S các nghiệm của phương trình (2cos2x+5)
(
sin
4
x
-
cos
4
x
)
+3 0 trong khoảng
0
;
2
π
A.
S
11
π
6
B. S4
π
C. S...
Đọc tiếp
Tính tổng S các nghiệm của phương trình (2cos2x+5) ( sin 4 x - cos 4 x ) +3 = 0 trong khoảng 0 ; 2 π
A. S = 11 π 6
B. S=4 π
C. S = 5
D. S = 7 π 6
Tính tổng S các nghiệm của phương trình
(
2
c
o
s
2
x
+
5
)
(
s
i
n
4
x
–
c
o
s
4
x
)
+
3
0
trong khoảng (0;2ᴨ) A.
S
11
π
6
B.
S...
Đọc tiếp
Tính tổng S các nghiệm của phương trình ( 2 c o s 2 x + 5 ) ( s i n 4 x – c o s 4 x ) + 3 = 0 trong khoảng (0;2ᴨ)
A. S = 11 π 6
B. S = 4 π
C. S = 5 π
D. S = 7 π 6
Tính tổng S các nghiệm của phương trình (2 cos2 x+5)
(
s
i
n
4
x
-
c
o
s
4
x
)
+30 trong khoảng
(
0
;
2
π
)
A. S11
π
/6 B. S4
π
C. S5
π
D. S7
π
/6
Đọc tiếp
Tính tổng S các nghiệm của phương trình (2 cos2 x+5) ( s i n 4 x - c o s 4 x ) +3=0 trong khoảng ( 0 ; 2 π )
A. S=11 π /6
B. S=4 π
C. S=5 π
D. S=7 π /6
Tính tổng S các nghiệm của phương trình
2
cos
2
x
+
5
sin
4
x
−
cos
4
x
+
3
0
trong khoảng
0
;
2...
Đọc tiếp
Tính tổng S các nghiệm của phương trình 2 cos 2 x + 5 sin 4 x − cos 4 x + 3 = 0 trong khoảng 0 ; 2 π .
A. S = 4 π .
B. S = 7 π 6 .
C. S = 11 π 6 .
D. S = 5 π .
Phương pháp:
Biến đổi về phương trình bậc 2 đối với cos2x. Sử dụng công thức nhân đôi: cos 2 x = cos 2 x − sin 2 x
Cách giải:
Ta có:
2 cos 2 x + 5 sin 4 x − cos 4 x + 3 = 0 ⇔ 2 cos 2 x + 5 sin 2 x − cos 2 x sin 2 x + cos 2 x + 3 = 0
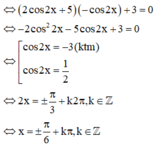
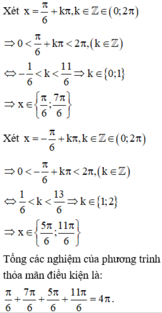
Chọn: A
Đúng 0
Bình luận (0)
Tính tổng S các nghiệm của phương trình
2
cos
2
x
+
5
sin
4
x
-
cos
4
x
+
3
0
trong khoảng
0
;
2...
Đọc tiếp
Tính tổng S các nghiệm của phương trình 2 cos 2 x + 5 sin 4 x - cos 4 x + 3 = 0 trong khoảng 0 ; 2 π .
A. S = 11 π 6
B. S = 4 π
C. S = 5 π
D. S = 7 π 6
Đáp án B.
PT ⇔ 2 cos 2 x + 5 sin 2 x - cos 2 x sin 2 x + cos 2 x + 3 = - 2 cos 2 x + 5 cos 2 x + 3 = 0
⇔ 2 cos 2 2 x + 5 cos 2 x - 3 = 0 ⇔ [ cos 2 x = - 3 ( ! ) cos 2 x = 1 2 ⇔ 2 x = ± π 3 + k 2 π
⇔ x = ± π 3 + k π ∈ 0 ; 2 π ⇔ x ∈ π 6 ; 5 π 6 ; 7 π 6 ; 11 π 6 ⇒ S = 4 π .
Đúng 0
Bình luận (0)
Tính tổng S các nghiệm của phương trình
2
cos
2
x
+
5
sin
4
x
-
cos
4
x
+
3
0
trong khoảng
0
;
20...
Đọc tiếp
Tính tổng S các nghiệm của phương trình 2 cos 2 x + 5 sin 4 x - cos 4 x + 3 = 0 trong khoảng 0 ; 2018 π
A. 2020.2018 π
B. 1010.2018 π
C. 2018.2018 π
D. 2016.2018 π
Tính tổng S các nghiệm của phương trình \(\left(2cos2x+5\right)\left(sin^4x-cos^4x\right)+3=0\) trong khoảng \(\left(0;2\pi\right)\)