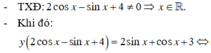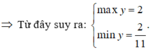tìm GTLN và GTNN của: A=5-32
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
DH
Những câu hỏi liên quan
Bài 1: Tìm GTNN và GTLN của \(A=123+\sqrt{-x^2+6x+5}\)
Bài 2:Tìm GTNN và GTLN của \(A=\sqrt{-x^2+8x-12}-7\)
Bài 3: Tìm GTNN và GTLN của \(A=\sqrt{-x^2-x+4}\)
Tìm GTLN và GTNN của hàm số
y
2
sin
x
+
cos
x
+
3
2
cos
x
-
sin
x
+
4
là: A.
m
i
n
y...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là:
A. m i n y = - 3 2 - 1 , m a x y = 3 2 + 1
B. m i n y = - 3 2 - 1 , m a x y = 3 2 - 1
C. m i n y = - 3 2 , m a x y = 3 2 - 1
D. m i n y = - 3 2 - 2 , m a x y = 3 2 - 1
Tìm GTLN, GTNN của hàm số
y
3
2
-
sin
x
+
1
A.
m
a
x
y
4
,
m
i
n
y
2
B.
m
a
x
y
3
,...
Đọc tiếp
Tìm GTLN, GTNN của hàm số y = 3 2 - sin x + 1
A. m a x y = 4 , m i n y = 2
B. m a x y = 3 , m i n y = 3 + 1
C. m a x y = 4 , m i n y = 3 + 1
D. m a x y = 3 , m i n y = 2
Tìm GTLN, GTNN của hàm số
y
3
2
-
sin
x
+
1
A. B. C. D.
Đọc tiếp
Tìm GTLN, GTNN của hàm số y = 3 2 - sin x + 1
A.![]()
B.![]()
C. ![]()
D.![]()
Tìm GTLN và GTNN của A= 3\(\sqrt{x-1}+4\sqrt{5-x}\) với 1≤x≤5
\(A\le\sqrt{\left(3^2+4^2\right)\left(x-1\right)\left(5-x\right)}=10\)
\(A_{max}=10\) khi \(\dfrac{\sqrt{x-1}}{3}=\dfrac{\sqrt{5-x}}{4}\Rightarrow x=\dfrac{61}{25}\)
\(A=3\left(\sqrt{x-1}+\sqrt{5-x}\right)+\sqrt{5-x}\ge3\left(\sqrt{x-1}+\sqrt{5-x}\right)\ge3\sqrt{x-1+5-x}=6\)
\(A_{min}=6\) khi \(x=5\)
Đúng 3
Bình luận (0)
a , Tìm GTNN của A = | x - 3 | + 50
b , Với giá trị nào của x thì biểu thức B = 1000 - | x + 5 | có GTLN với GTLN đó
c , Tìm GTNN của C = ( x - 2016 ) ^2 - 2017
d, với giá trị nào của x và y thì biểu thức D = | x - 100 | ^ 3 + | y + 200 | - 1 có GTNN và tìm GTNN đó
Mong các bn giai giúp mk nha mk đang cân gấp
Vì | x -3 | > hoặc = 0
Suy ra : |x-3|+50 >hoặc =50
Vì A nhỏ nhất suy ra | x-3 | +50 =50
Suy ra x-3 =0
Suy ra x=3
Vậy GTNN của A = 50 khi x=3
Đúng 0
Bình luận (0)
Cho x,y thuộc Z:
a)Với giá trị nào của x thì biểu thức A=1000- |x+5| có GTLN;tìm GTLN đó.
b)Với giá trị nào của y thì biểu thức B=|y-3|+50 có GTNN;tìm GTNN đó.
c)Với giá trị nào của x và y thì biểu thức C=|x-100| +|y+200| -1 có GTNN;tìm GTNN đó.
Chỉ mình cách tìm GTLN hay GTNN của biểu thức được không?
VD: Tìm GTLN của A = 1 - x^2 + 3*x
Tìm GTNN của B = x^2 - 5*x + 1
Tìm GTLN và GTNN của hàm số
y=3sinx + 4cosx + 5
A. min y = 0, max y= 13
B. min y =0, max y=10
C. min y= 1, max y=10
D. Tất cả sai
Tìm GTLN của Q=\(-2x^2+6x+8\)
Tìm GTLN và GTNN của: A=\(\dfrac{6x+17}{x^2+2}\)
\(Q=-2\left(x-\dfrac{3}{2}\right)^2+\dfrac{25}{2}\le\dfrac{25}{2}\)
\(Q_{max}=\dfrac{25}{2}\) khi \(x=\dfrac{3}{2}\)
\(A=\dfrac{9\left(x^2+2\right)-9x^2+6x-1}{x^2+2}=9-\dfrac{\left(3x-1\right)^2}{x^2+2}\le9\)
\(A_{max}=9\) khi \(x=\dfrac{1}{3}\)
\(A=\dfrac{12x+34}{2\left(x^2+2\right)}=\dfrac{-\left(x^2+2\right)+x^2+12x+36}{2\left(x^2+2\right)}=-\dfrac{1}{2}+\dfrac{\left(x+6\right)^2}{2\left(x^2+2\right)}\le-\dfrac{1}{2}\)
\(A_{min}=-\dfrac{1}{2}\) khi \(x=-6\)
Đúng 1
Bình luận (0)