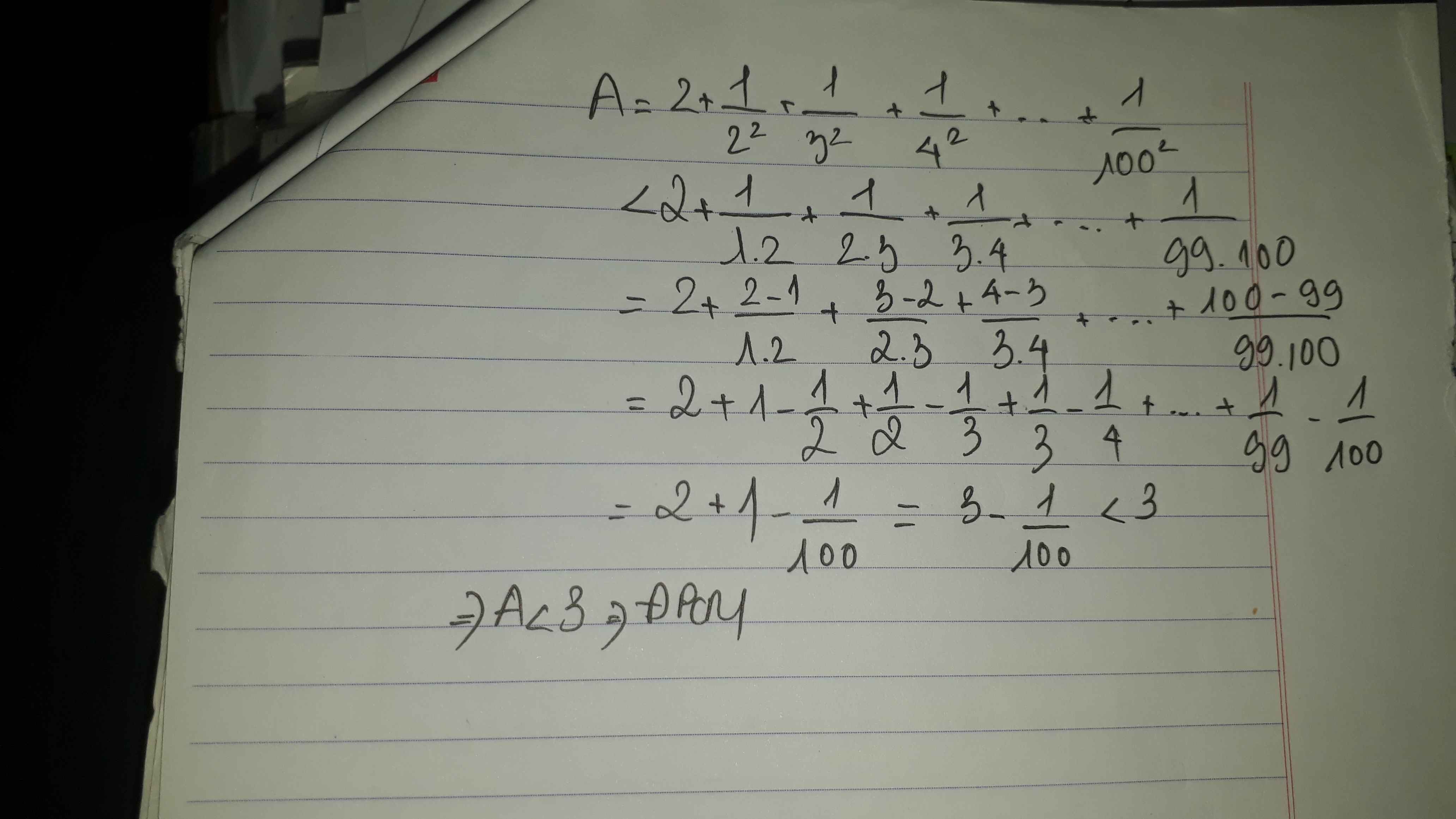Cho A = 1/2^2+1/3^2+1/4^2+...+1/100^2. Hãy chứng tỏ rằng 1/2<A <4/5
CL
Những câu hỏi liên quan
Hãy chứng tỏ rằng : 100-[1+1/2+1/3+...+1/100] = 1/2+2/3+3/4+...+99/100
Mình cần gấp
Ta có : \(\frac{1}{2}+\frac{2}{3}+..+\frac{99}{100}\)
= \((1-\frac{1}{2})+(1-\frac{1}{3})+...+(1-\frac{99}{100})\)(100 cặp số )
= \(\left(1+1+1+...+1\right)-\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\right)\)(100 số hạng 1)
= \(1\times100-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+..+\frac{1}{100}\right)\)
= \(100-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{100}\right)\)
=> 100-(1+1/2+1/3+...+1/100) = 1/2+2/3+3/4+...+99/100
Đúng 3
Bình luận (0)
Bạn cố giải cho mình dễ hiểu hơn ko?
Đúng 0
Bình luận (0)
Cho A=1+1/2+1/3+1/4+...+1/2^100-1.Chứng tỏ rằng 50<A<100
Cho A=1/2^2+1/3^2+1/4^2+...+1/100^2
Hãy chứng tỏ A<3/4
Cho A = 1/2^2 + 1/3^2 + 1/4^2 + ........ + 1/100^2
Chứng tỏ rằng 3/5 < A < 3/4
Không spam nha. Chương trình game xin tặng chương trình học online. Nhằm mục đích game được nhiều người chơi.
Thay mặt người đào tạo chương trình hôm nay : Có 200 suất học bỗng cho những học sinh tích cực hoạt động từ bây giờ ( Mỗi suất học bỗng là 100k). Nhận thưởng bằng cách vào google tìm kiếm.
Link như sau vào google hoặc cốc cốc để tìm kiếm:
https://lazi.vn/quiz/d/17912/game-lien-quan-mobile-ra-doi-vao-ngay-thang-nam-nao
Copy cũng được nha
Bạn hack nick mình thu ib dưới vs nha giúp mk chuyện này:))
Đúng 0
Bình luận (0)
Bài 1:
a) Chứng tỏ rằng : 200 - (3+2/3+2/4+....+2/100)
--------------------------------------- = 2
1/2+2/3+3/4+....+9/100
b) Cho B =5/2.1 + 4/1.11 + 3/11.2 + 1/2.15 + 15/4.43 + 13/43
Chứng tỏ rằng B > 3
BB
18 tháng 7 2021 lúc 20:40
Chứng tỏ rằng: A= 2+\(\dfrac{1}{2^2}\)+\(\dfrac{1}{3^2}^{ }\)+\(\dfrac{1}{4^2}\)+...+\(\dfrac{1}{100^2}\)<3
TQ
25 tháng 4 2023 lúc 9:53
Chứng tỏ rằng:
a)\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{3}{4}\)
b)\(\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\)
b\()\)
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2.3 + 1/3.4 +... + 1/99.100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/3 + 1/3 -1/4 +... + 1/99 + 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 3/4 - 1/100 < 3/4
Đúng 2
Bình luận (0)
Tương tự như vậy với câu a\()\)
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2.3 + 1/3.4 +... + 1/99.100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/3 + 1/3 -1/4 +... + 1/99 + 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 3/4 - 1/100 < 1/2
Đúng 0
Bình luận (0)
chứng tỏ rằng:1/2^2+1/3^2+1/4^2+...+1/99^2+1/100^2<3/4
a, Chứng tỏ rằng: \(\dfrac{12n+1}{30n+2}\) là phân số tối giản.
b, Chứng minh rằng: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1\)
a) Gọi ƯCLN(12n+1,30n+2) là d
12n+1⋮d ⇒ 60n+5⋮d
30n+2⋮d ⇒ 60n+4⋮d
(60n+5)-(60n+4)⋮d
1⋮d
Vậy \(\dfrac{12n+1}{30n+2}\) là ps tối giản
Đúng 1
Bình luận (0)
b) Đặt A=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}\)
Ta có: \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}< 1\left(đpcm\right)\)
Đúng 1
Bình luận (0)