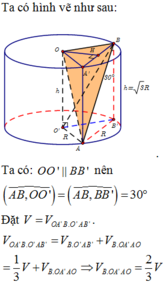
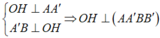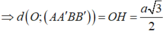cho hình trụ (H) có (O;R) và (O';R') là 2 hình tròn. Hình nón (N) có đỉnh O và đáy (O';R'). Tính V(H)/V(N)
LV
Những câu hỏi liên quan
Cho hình trụ có hai đường tròn đáy (O;R) và(O’;R), chiều cao
h
3
R
. Đoạn thẳng AB có hai đầu mút nằm trên hai đường tròn đáy hình trụ sao cho góc hợp bởi AB và trục của hình trụ là α30 độ. Thể tích tứ diện ABOO’ là: A.
R
3
4
B.
R
3
2...
Đọc tiếp
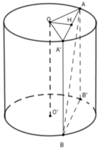
Cho hình trụ có hai đường tròn đáy (O;R) và(O’;R), chiều cao h = 3 R . Đoạn thẳng AB có hai đầu mút nằm trên hai đường tròn đáy hình trụ sao cho góc hợp bởi AB và trục của hình trụ là α=30 độ. Thể tích tứ diện ABOO’ là:
A. R 3 4
B. R 3 2
C. 3 R 3 2
D. 3 R 3 4
Cho hình trụ có hai đáy là hai hình tròn
O
và
O
, chiều cao
h
a
3
và bán kính đáy
R
a
. Một hình nón có đỉnh là O và đáy là hình tròn . Tỉ số diện tích xung quanh của hình trụ và hình nón bằng A. 3 B.
2
C. 2 D.
3
Đọc tiếp
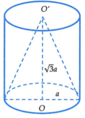
Cho hình trụ có hai đáy là hai hình tròn O và O ' , chiều cao h = a 3 và bán kính đáy R = a . Một hình nón có đỉnh là O' và đáy là hình tròn . Tỉ số diện tích xung quanh của hình trụ và hình nón bằng
A. 3
B. 2
C. 2
D. 3
Cho hình trụ (H) có đáy là hai đường tròn tâm O và O', bán kính đáy R = OO'. Trên đáy tâm O lấy điểm A, trên đáy tâm O' lấy điểm B sao cho AB = 2R. Tính tỉ số thể tích giữa khối tứ diện ABOO' và khối trụ (H) ?
Cho hình trụ có tâm hai đáy lần lượt là O và O ; bán kính đáy hình trụ bằng a.Trên hai đường tròn (O) và (O) lần lượt lấy hai điểm A và B sao cho đường thẳng AB tạo với trục của hình trụ một góc
30
°
và có khoảng cách tới trục của hình trụ bằng
a
3
2
.Tính diện tích toàn phần của hình trụ đã cho. A. ...
Đọc tiếp
Cho hình trụ có tâm hai đáy lần lượt là O và O' ; bán kính đáy hình trụ bằng a.Trên hai đường tròn (O) và (O') lần lượt lấy hai điểm A và B sao cho đường thẳng AB tạo với trục của hình trụ một góc 30 ° và có khoảng cách tới trục của hình trụ bằng a 3 2 .Tính diện tích toàn phần của hình trụ đã cho.
A. π a 2 3 3 + 2
B. π a 2 3 + 2
C. 2 π a 2 3 + 1
D. 2 π a 2 3 3 + 3
Cho hình trụ có tâm hai đáy lần lượt là O và O; bán kính đáy hình trụ bằng a. Trên hai đường tròn (O) và (O) lần lượt lấy hai điểm A và B sao cho AB tạo với trục của hình trụ một góc
30
°
và có khoảng cách tới trục của hình trụ bằng
a
3
2
. Tính diện tích toàn phần của hình trụ đã cho
Đọc tiếp
Cho hình trụ có tâm hai đáy lần lượt là O và O'; bán kính đáy hình trụ bằng a. Trên hai đường tròn (O) và (O') lần lượt lấy hai điểm A và B sao cho AB tạo với trục của hình trụ một góc 30 ° và có khoảng cách tới trục của hình trụ bằng a 3 2 . Tính diện tích toàn phần của hình trụ đã cho
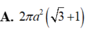
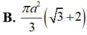
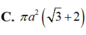
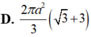
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SOh không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính ROA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
Đọc tiếp
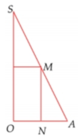
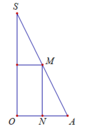
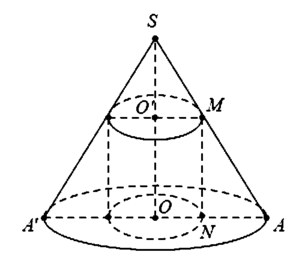
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO=h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R=OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
![]()
![]()
![]()
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất A. MN h/2 B. MN h/3 C. MN h/4 D. MN h/6
Đọc tiếp
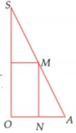
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
A. MN = h/2
B. MN = h/3
C. MN = h/4
D. MN = h/6
Đáp án B.
Khi quay hình vẽ quanh trục SO sẽ tạo nên khối trụ nội tiếp hình nón.
Suy ra thiết diện qua trục của hình trụ là hình chữ nhật MNPQ.
Theo định lí Talet, ta có 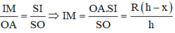
Thể tích khối trụ là 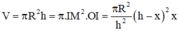
Theo AM – GM ta được
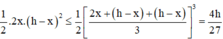
Vậy 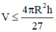 . Dấu “=” xảy ra khi
. Dấu “=” xảy ra khi 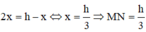
Đúng 0
Bình luận (0)
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên dưới. Đặt
S
O
h
không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính
R
O
A
. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất. A.
M
N
h
3
B...
Đọc tiếp
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên dưới. Đặt S O = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = O A . Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
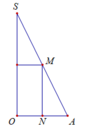
A. M N = h 3
B. M N = h 4
C. M N = h 6
D. M N = h 2
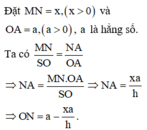
Khối trụ thu được có bán kính đáy bằng ON và chiều cao bằng MN.
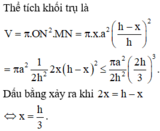
Chọn A
Đúng 0
Bình luận (0)
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất A.
M
N
h
2
B.
M
N
h
3
C.
M
N...
Đọc tiếp
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
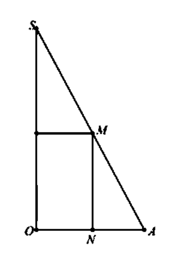
A. M N = h 2
B. M N = h 3
C. M N = h 4
D. M N = h 6
Đáp án B
Đặt SO' = x. Theo định lí Talet ta có:
x
h
=
r
'
r
0
<
x
<
h
Thể tích khối trụ là V = πr ' 2 h - x = π xr 2 h 2 h - x = f x
Ta có f x = πr 2 h 2 x 2 h - x
Cách 1. Xét M x = x 2 h - x
Cách 2. Ta có M x = 4 . x 2 . x 2 . h - x ≤ 4 x 2 + x 2 + h - x 3 3 = 4 h 3 27
Dấu “=” xảy ra ⇔ x 2 = h - x ⇔ x = 2 3 h ⇒ M N = h - x = h 3 .
Đúng 0
Bình luận (0)