Tìm hai số a và b biết chúng có tổng bằng 3 và tích bằng 1.
TH
Những câu hỏi liên quan
1.Tìm hai số tự nhiên a và b (a > b) có tổng bằng 224,biết rằng ƯCLN của chúng bằng 28
2.tìm hai số tự nhiên a và b(a>b) có tích bằng 1944,biết rằng ƯCLN của chúng bằng 18
Bài 1 : Tìm hai số biết tổng gấp 3 lần hiệu và bằng nửa tích của chúng .
Bài 2 : Tìm hai số biết tổng gấp 5 lần hiệu và bằng 1/6 tích của chúng .
Bài 1: Tổng trừ hiệu chính bằng hai lần số bé, từ đề bài ta suy ra 2 lần hiệu bằng hai lần số bé. Nói cách khác hiệu bằng số bé hay số lớn gấp đối số bé.
Tích của số bé và số lớn chính là tích số bé và hai lần số bé chia 2 hay chính bằng số bé nhân số bé. Tổng bằng 3 lần số bé và bằng số bé nhân số bé nên số bé bằng 3 và số lớn bằng 6.
Bài 2: Tương tự. Ta tìm được số bé là 10, số lớn là 15.
Đúng 0
Bình luận (0)
17 .3
tìm hai số tư nhiên a và b (a>b) có tổng bằng 224 biết rằng ƯCLN của chúng bằng 28
17.4
tìm hai số tự nhiên a và b ( a>b) có tích bằng 1944 biết rằng ƯCLN của chúng bằng 18
17.5
tìm số tự nhiên a biết rằng 156 chia cho a dư 12 và 280 chia cho a dư 10
1.vì ƯCLN 2 số là 28 nên đặt a=28k, b=28p, k,p là số tự nhiênta có 28(k+p)=224=>k+q=8vậy các cặp (a, b) thỏa mãn là (28,196), (56, 168), (84,140), (112, 112)và các hoán vị của nó.
2.Dựa vào dữ kiện đề bài,ta có:
a=18k;b=18p.(k,p nguyên tố cùng nhau)
Tích:a.b=18k.18p
=324.k.p=1944
=>k.p=6.
=>k bằng 3;p=2.
Vậy a=54;p=36.
3.ĐK a > 12 ( số chia phải lớn hơn dư )
156 chia a dư 12 => 156 - 12 chia hết cho a => 144 chia hết cho a (1)
280 chia a dư 10 => 280 - 10 chia hết cho a => 270 chia hết cho a (2)
Từ (1) và (2) => 144 ; 270 chia hết cho a
=> a thuộc UC (144;270)
UCLN ( 144 ; 270 ) = 18
=> a thuộc ( 18 ; 9 ; 6 ; 3 ; 1 )
a > 12 => a= 18
bài 1 ; tìm tích của hai số , biết rằng nếu giữ nguyên thừa số thứ nhất và tăng thừa số thứ hai lên 4 thì được tích mới là 8400 .
bài 2 ; tìm hai số biết tổng gấp 5 lần hiệu và bằng 1/6 tích của chúng .
bài 3 ; tìm hai số biết tổng gấp 3 lần hiệu và bằng nửa tích của chúng .
Tìm hai số nguyên sao cho tổng của chúng và tích của chúng là hai số đối nhau
tìm hai số nguyên a và b biết tổng của chúng bằng 3 lần hiệu a chia b còn thương a chia b và hiệu ai trừ b là hai số đối nhau
tìm hai phân số tối giản có tử và mẫu là số tự nhiên biết
a) tổng của chúng bằng tích của chúng
b) hiệu của chúng bằng tích của chúng
a. 7/2 và 7/5
mìh chỉ giải được câu a thui bạn thông cảm
Đúng 0
Bình luận (0)
Bài 1:Tìm hai số tự nhiên.Biết rằng tổng của chúng bằng 66,ước chung lớn nhất của chúng bằng 6,đồng thời có một số chia hết cho 5.
Bài 2:Tìm hai số tự nhiên ,biết hiệu của chúng bằng 84 và ước chung lớn nhất của chúng bằng 12.
Bài 3:Tìm hai số tự nhiên,biết tích của chúng bằng 864 và ước chung lớn nhất của chúng bằng 6.
Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4.
Hai số phức có tổng bằng 3, tích bằng 4 là nghiệm của phương trình:
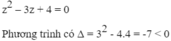
⇒ Phương trình có hai nghiệm: 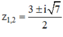
Vậy hai số cần tìm là 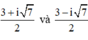
Đúng 0
Bình luận (0)
1.Tổng của hai số tự nhiên gấp 3 lần hiệu của chúng .Tìm thương của hai số tự nhiên đó2.Khi chia số tự nhiên a cho 54 ta được số dư 38.Chia số a cho 18 ta được thương 14 và còn dư .Tìm số a3.a)Có ba số tự nhiên nào mà tổng của chúng tận cùng bằng 4 ,tích của chúng tận cùng bằng 1 hay không?b)Có tồn tại hay không 4 số tự nhiên mà tổng và tích của chúng đều là số lẻ?
Đọc tiếp
1.Tổng của hai số tự nhiên gấp 3 lần hiệu của chúng .Tìm thương của hai số tự nhiên đó
2.Khi chia số tự nhiên a cho 54 ta được số dư 38.Chia số a cho 18 ta được thương 14 và còn dư .Tìm số a
3.a)Có ba số tự nhiên nào mà tổng của chúng tận cùng bằng 4 ,tích của chúng tận cùng bằng 1 hay không?
b)Có tồn tại hay không 4 số tự nhiên mà tổng và tích của chúng đều là số lẻ?
1) Gọi hai số đó là a và b
Ta có: a+b=3(a-b)
=> a+b = 3a -3b
=> a+b +3b = 3a
=> a+ 4b = 3a => 4b = 2a => 2b = a => a : b = 2
ĐS : 2
2) Gọi thương của phép chia A chia cho 54 là b
Ta có : a : 54 = b ( dư 38 ) => a = 54b + 38
=> a = 18.3b + 18.2 + 2 = 18.( 3b + 2 ) + 2
=> a chia cho 18 được thương là 3b + 2 ; dư 2
Theo đề bài 3b + 2 = 14 => 3b = 12 => b = 4
Vậy a = 54.4 + 38 = 254
3)a) Tích của 3 số tận cùng là 1 => tích lẻ => cả 3 số trong đó đều là số lẻ
Mà Tổng của 3 số lẻ là 1 số lẻ nên không thể tận cùng là 4
=> Không tồn tại 3 số như vậy
b) Tích 4 số là số lẻ => cả 4 số đó đều là số lẻ
Vì tổng của 2 số lẻ là số chẵn nên tổng của 4 số lẻ là số chẵn => Không tồn tại 4 số thỏa mãn tổng là số lẻ
~ Học tốt ~
Đúng 0
Bình luận (0)
Tìm hai số a và b khác 0 biết rằng tổng và hiệu của chúng lần lượt tỉ lệ với 6 và 1 và tích của chúng bằng 35

