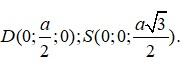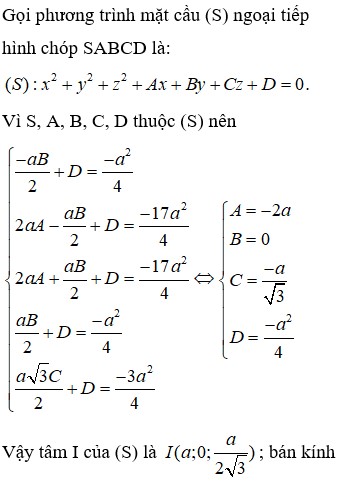Cho hình chóp SABCD có đáy là hình chữ nhật với AB=2a;AD=a. Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng(SBC) và (ABCD) bằng 450 . Khi đó thể tích khối chóp SABCD là
KT
Những câu hỏi liên quan
LV
8 tháng 6 2021 lúc 21:17
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Bạn chỉ nên đăng 1 bài 1 lần thôi, tránh làm loãng box toán!
Đúng 1
Bình luận (0)
LV
8 tháng 6 2021 lúc 22:05
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Lời giải:
Vì $SA\perp (ABCD)$ nên
$60^0= \angle (SC, (ABCD))=\angle (SC, AC)=\widehat{SCA}$
Ta có:
$AC=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
$\frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{15}a$
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}$
$=\frac{1}{3}.\sqrt{15}a.a.2a=\frac{2\sqrt{15}}{3}a^3$
Đúng 2
Bình luận (0)
Cho hình chóp SABCD có đáy là hình chữ nhật tâm O với AB2a, BCa. Các cạnh bên của hình chóp đều bằng nhau và bằng
a
2
. Thể tích hình chóp SABCD bằng A.
a
3
3
2
B.
a
3
3
3
C. ...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình chữ nhật tâm O với AB=2a, BC=a. Các cạnh bên của hình chóp đều bằng nhau và bằng a 2 . Thể tích hình chóp SABCD bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 4
D. a 3 3 5
Cho hình chóp SABCD có đáy là hình chữ nhật, AB2a, BCa. Hình chiếu vuông góc của S trên (ABCD) là trung điểm H của AD,
S
H
a
3
2
. Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD A.
4
πa
2
3
B.
16
πa...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình chữ nhật, AB=2a, BC=a. Hình chiếu vuông góc của S trên (ABCD) là trung điểm H của AD, S H = a 3 2 . Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD
A. 4 πa 2 3
B. 16 πa 2 3
C. 16 πa 2 3
D. 4 πa 3 3
cho hình chóp sabcd có đáy abcd là hình chữ nhật,ab=a,ad=2a,sa vuông góc với mặt phẳng đáy,góc giữa sb và đáy bằng 45 độ,độ dài cạnh sd là
Lời giải:
Do $SA\perp (ABCD)$ nên $\angle (SB, ABCD)=\angle (SB, AB)=\widehat{SBA}=45^0$
$\Rightarrow SAB$ là tam giác vuông cân tại $A$
$\Rightarrow SA=AB=a$
Áp dụng định lý Pitago: $SD=\sqrt{SA^2+AD^2}=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
Đúng 0
Bình luận (0)
LV
22 tháng 6 2021 lúc 22:51
cho hình chóp SABCD đáy là hình chữ nhật. AB=a, AD=2a, tam giác SAB cân tại S và (SAB) vuông góc với đáy. Góc giữa SC và đáy là 45°. Tính thể tích SABCD/a³ căn 17
LV
22 tháng 6 2021 lúc 21:51
cho hình chóp SABCD đáy là hình chữ nhật. AB=a, AD=2a, tam giác SAB cân tại S và (SAB) vuông góc với đáy. Góc giữa SC và đáy là 45°. Tính thể tích SABCD/a³ căn 17
Lời giải:
Lấy $H$ là trung điểm $AB$ thì do $SAB$ cân tại $S$ nên $SH\perp BH$
$BH$ là giao tuyến của $(SAB), (ABCD)$; (SAB)\perp (ABCD)$ nên $SH\perp (ABCD)$
$\Rightarrow (SC, (ABCD))=(SC, CH)=\widehat{SCH}=45^0$
$\Rightarrow SH=CH=\sqrt{BC^2+BH^2}=\sqrt{(2a)^2+(\frac{a}{2})^2}=\frac{\sqrt{17}}{2}a$
\(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{17}}{2}a.a.2a=\frac{\sqrt{17}}{3}a^3\)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD có đáy là hình chữ nhật
A
B
2
a
,
A
D
2
a
, SA vuông góc với đáy và
S
A
2
a
Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng A.
1
3
B.
3...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình chữ nhật A B = 2 a , A D = 2 a , SA vuông góc với đáy và S A = 2 a Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng
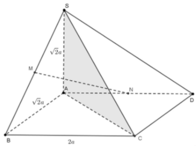
A. 1 3
B. 3 3
C. 6 3
D. 3 6
Chọn gốc toạ độ tại A. Các tia Ox; Oy; Oz lần lượt trùng với các tia AD, AB, AS ta có tọa độ điểm là A(0;0;0); D(2;0;0); B ( 0 ; 2 ; 0 ) ; S ( 0 ; 0 ; 2 ) ; C 2 ; 2 ; 0 ; M 0 ; 2 2 ; 2 2 ; N 1 ; 0 ; 0
Do vậy
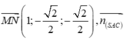
và
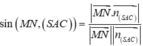
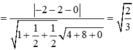
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy hình chữ nhật AB=a, BC=2a, SA vuông góc với ABCD, SA= acăn5. Tính khoảng cách từ C đến mp SAD.
Theo đề có:
\(\left\{{}\begin{matrix}CD\perp AD\\CD\perp SA\end{matrix}\right.\)
=> \(CD\perp\left(SAD\right)\)
<=> \(d\left(C,\left(SAD\right)\right)=CD=a\)
`HaNa♬`
Đúng 1
Bình luận (0)
Cho hình chóp SABCD, SA vuông góc (ABCD) , ABCD là hình chữ nhật có AB = a , AD 2a , góc hợp bởi (SBC) và đáy là 60° . Tính chiều cao và thể tích khối chóp