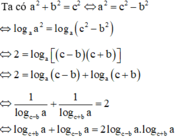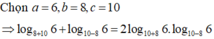cho a,b,c là độ dài 3 cạnh tam giác vuông a là cạnh huyền tính Max Q=(1+b/a)(1+c/a)
DT
Những câu hỏi liên quan
Cho a,b,c là các cạnh của tam giác vuông , h là độ daif đường cao ứng với cạnh huyền a . Chứng minh tam giác có độ dài 3 canh a+h , b+c và h là độ dài 3 cạnh tam giấc vuông.
Ký hiệu:
AB=c; AC=b; cạnh huyền BC=a; đường cao CH=h Ta có
Xét hai t/g vuông AHC và ABC có
\(\widehat{C}\)chung
\(\widehat{CAH}=\widehat{ABC}\)(cùng phụ với \(\widehat{C}\))
=> t/g AHC đồng dạng với ABC \(\Rightarrow\frac{b}{a}=\frac{h}{c}\Rightarrow bc=ah\)
Xét t/g vuông ABC có
\(b^2+c^2=a^2\Rightarrow\left(b+c\right)^2=a^2+2bc\)
\(\Rightarrow\left(b+c\right)^2=a^2+2ah\)( bc=ah chứng minh trên)
\(\Rightarrow\left(b+c\right)^2=\left(a^2+2ah+h^2\right)-h^2=\left(a+h\right)^2-h^2\)
\(\Rightarrow\left(b+c\right)^2+h^2=\left(a+h\right)^2\)
=> b+c; a+h; h là 3 cạnh của tam giác vuông trong đó cạnh huyền là a+h
Đúng 0
Bình luận (0)
Sorry!!!
Phần ký hiệu sửa thành
Đường cao AH=h
Đúng 0
Bình luận (0)
Bài 1:Cho a=4m+8n+9p
b=m+4n+4p
c=4m+7n+8p
Với m,n,p là độ dài 3 cạnh của 1 tam giác vuông(p là cạnh huyền)
CMR a,b,c cũng là độ dài 3 cạnh của 1 tam giác vuông
Vì m, n, p là độ dài 3 cạnh tam giác vuông (p là cạnh huyền) nên
p2 = m2 + n2
Ta có: a2 - b2 - c2 = (4m + 8n + 9p)2 - (m + 4n + 4p)2 - (4m + 7n + 8p)2
= - n2 + p2 - m2 = 0
=> a2 = b2 + c2
Vậy a, b, c cũng là độ dài ba cạnh tam giác vuông. Và cạnh huyền là a
Đúng 0
Bình luận (0)
Cho a, b, là độ dài hai cạnh góc vuông c, là độ dài cạnh huyền của một tam giác vuông và
c
-
b
≠
1
,
c
+
b
≠
1
. Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho a, b, là độ dài hai cạnh góc vuông c, là độ dài cạnh huyền của một tam giác vuông và c - b ≠ 1 , c + b ≠ 1 . Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Đáp án B
Từ giả thiết ta có a2 + b2 = c2
Đúng 0
Bình luận (0)
Cho a b, là độ dài hai cạnh góc vuông c, là độ dài cạnh huyền của một tam giác vuông và
c
−
b
≠
1
,
c
+
b
≠
1.
Mệnh đề nào sau đây đúng? A.
log
c
+
b
a
+
log
c
−
b
a
log...
Đọc tiếp
Cho a b, là độ dài hai cạnh góc vuông c, là độ dài cạnh huyền của một tam giác vuông và c − b ≠ 1 , c + b ≠ 1. Mệnh đề nào sau đây đúng?
A. log c + b a + log c − b a = log c + b a . log c − b a
B. log c + b a + log c − b a = 2 log c + b a . log c − b a
C. log c + b a + log c − b a = log c + b c − b
D. log c + b a + log c − b a = log c + b 2 a . log c − b 2 b
Đáp án B
Từ giả thiết ta có a 2 + b 2 = c 2
log c + b a + log c − b a = 1 log a c + b + 1 log a c − b = log a c + b + log a c − b log a c + b log a c − b = log a c 2 − b 2 log a c + b log a c − b = log a a 2 log a c + b log a c − b = 2 log a c + b log a c − b = 2 log c + b a . log c − b a
Đúng 0
Bình luận (0)
cho a,b,c là độ dài 3 cạnh một tam giác vuông và a là cạnh huyền. Chứng minh \(a^3>b^3+c^3\)
cho a,b,c là độ dài 3 cạnh một tam giác vuông và a là cạnh huyền. Chứng minh rằng: \(a^3>b^3+c^3\)
Cho tam giác vuông ABC có a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền, trong đó
c
−
b
≠
1
v
à
c
+
b
≠
1
. Hệ thức nào sau đây là đúng? A.
log
c
+
b
a
+
log
c
−
b
a...
Đọc tiếp
Cho tam giác vuông ABC có a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền, trong đó c − b ≠ 1 v à c + b ≠ 1 . Hệ thức nào sau đây là đúng?
A. log c + b a + log c − b a = 2 log c 2 − b 2 a .
B. log c + b a + log c − b a = log c 2 − b 2 a .
C. log c + b a + log c − b a = 2 log c + b a . log c − b a
D. log c + b a + log c − b a = log c + b a . log c − b a
Cho a ; b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của một tam giác vuông. Trong đó
c
−
b
≠
1
và
c
+
b
≠
1
. Kết luận nào sau đây là đúng ? A.
log
c
+
b
a
+
lo...
Đọc tiếp
Cho a ; b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của một tam giác vuông. Trong đó c − b ≠ 1 và c + b ≠ 1 . Kết luận nào sau đây là đúng ?
A. log c + b a + log c − b a = 2 log c + b a log c − b a
B. log c + b a + log c − b a = log c + b a log c − b a
C. log c + b a + log c − b a = − 2 log c + b a log c − b a
D. log c + b a + log c − b a = − log c + b a log c − b a
Cho tam giác vuông ABC có a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền, trong đó c-b khác 1 và c+b khác 1. Hệ thức nào sau đây là đúng? A.
log
c
+
b
a
+
log
c
−
b
a
2
log
c...
Đọc tiếp
Cho tam giác vuông ABC có a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền, trong đó c-b khác 1 và c+b khác 1. Hệ thức nào sau đây là đúng?
A. log c + b a + log c − b a = 2 log c 2 − b 2 a .
B. log c + b a + log c − b a = log c 2 − b 2 a .
C. log c + b a + log c − b a = 2 log c + b a . log c − b a
D. log c + b a + log c − b a = log c + b a . log c − b a .
Cho a,b,c là độ dài ba cạnh của một tam giác vuông(c là độ dài cạnh huyền).Chứng minh rằng a^2020+b^2020<c^2020