Mọi người giải dùm mình với
SD
Những câu hỏi liên quan
 mọi người giải rõ ràng ra dùm mình với
mọi người giải rõ ràng ra dùm mình với
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{36}=\dfrac{b}{38}=\dfrac{a+b}{36+38}=\dfrac{222}{74}=3\)
Do đó: a=108; b=114
Đúng 0
Bình luận (0)
\(\text{Gọi x;y lần lượt là số dây đeo khẩu trang lớp 7A,7B:}\)
(đk:x;y\(\in\)N*,đơn vị:dây đeo khẩu trang)
\(\text{Ta có:}\dfrac{x}{36}=\dfrac{y}{38}\text{ và }x+y=222\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{36}=\dfrac{y}{38}=\dfrac{x+y}{36+38}=\dfrac{222}{74}=3\)
\(\Rightarrow x=3.36=108\text{(dây đeo khẩu trang)}\)
\(y=3.38=114\text{(dây đeo khẩu trang)}\)
\(\text{Vậy số dây đeo khẩu trang lớp 7A là:108 dây đeo khẩu trang}\)
\(\text{lớp 7B là:114 dây đeo khẩu trang}\)
Đúng 0
Bình luận (0)
Giải hôn dùm mình đi mọi người ơi

1 C
2 C
3 D
4 A
5 D
6 D
7
8 A
9 C
10 D
( Câu 7 đáp án sai hay sao á bạn )
Đúng 0
Bình luận (3)
Tự luận em cần hỗ trợ hết à em?
Đúng 0
Bình luận (1)
GIÚP MÌNH VỚI MỌI NGƯỜI ƠI TRẢ LỜI KÈM GIẢI THÍCH DÙM MÌNH MỌI NGƯỜI ƠI Choose the word whose underlined part is pronounced differently from the others.3.A. goneB. blankC. sandD. bent4.A. shownB. knitC. lineD. drink
Đọc tiếp
GIÚP MÌNH VỚI MỌI NGƯỜI ƠI TRẢ LỜI KÈM GIẢI THÍCH DÙM MÌNH MỌI NGƯỜI ƠI
Choose the word whose underlined part is pronounced differently from the others.
3.A. gone | B. blank | C. sand | D. bent |
4.A. shown | B. knit | C. line | D. drink |
3.A. gone | B. blank ( cái này âm NG còn lại là âm n ) | C. sand | D. bent |
4.A. shown | B. knit | C. line | D. drink ( lời giải thích giống câu trên ) |
Đúng 4
Bình luận (0)
Đáp án:
3. B (âm ŋ còn lại âm n)
4. D (âm ŋ còn lại âm n)
Đúng 1
Bình luận (0)
Choose the word which has a different stress pattern from that of the others1.A. persuadeB. albumC. guitarD. anxious2.A. entertainmentB. phenomenonC. enthusiasticD. original GIÚP MÌNH VỚI MỌI NGƯỜI ƠI TRẢ LỜI KÈM GIẢI THÍCH DÙM MÌNH MỌI NGƯỜI ƠI
Đọc tiếp
Choose the word which has a different stress pattern from that of the others
1.A. persuade | B. album | C. guitar | D. anxious |
2.A. entertainment | B. phenomenon | C. enthusiastic | D. original |
GIÚP MÌNH VỚI MỌI NGƯỜI ƠI TRẢ LỜI KÈM GIẢI THÍCH DÙM MÌNH MỌI NGƯỜI ƠI
Choose the word which has a different stress pattern from that of the others
1. Đề sai (vì A,C nhấn âm 2, còn B,D nhấn âm 1)
2. Đề sai ;-;
Đúng 1
Bình luận (0)
Choose the word which has a different stress pattern from that of the others1.A. persuadeB. albumC. guitarD. anxious2.A. entertainmentB. phenomenonC. enthusiasticD. original GIÚP MÌNH VỚI MỌI NGƯỜI ƠI TRẢ LỜI KÈM GIẢI THÍCH DÙM MÌNH MỌI NGƯỜI ƠI
Đọc tiếp
Choose the word which has a different stress pattern from that of the others
1.A. persuade | B. album | C. guitar | D. anxious |
2.A. entertainment | B. phenomenon | C. enthusiastic | D. original |
GIÚP MÌNH VỚI MỌI NGƯỜI ƠI TRẢ LỜI KÈM GIẢI THÍCH DÙM MÌNH MỌI NGƯỜI ƠI
1.A. per'suade | B. 'album | C. gui'tar | D. 'anxious |
2.A. enter'tainment | B. phe'nomenon | C. enthusi'astic | D. o'riginal |
ngẫm ra thì thấy 2 câu này chẳng có câu nào có đáp án em à!
Đúng 0
Bình luận (0)
Mọi người giải dùm mình nha mình đang cần gấp để giải tiếp bài hóa 😿, mình cảm ơn ạ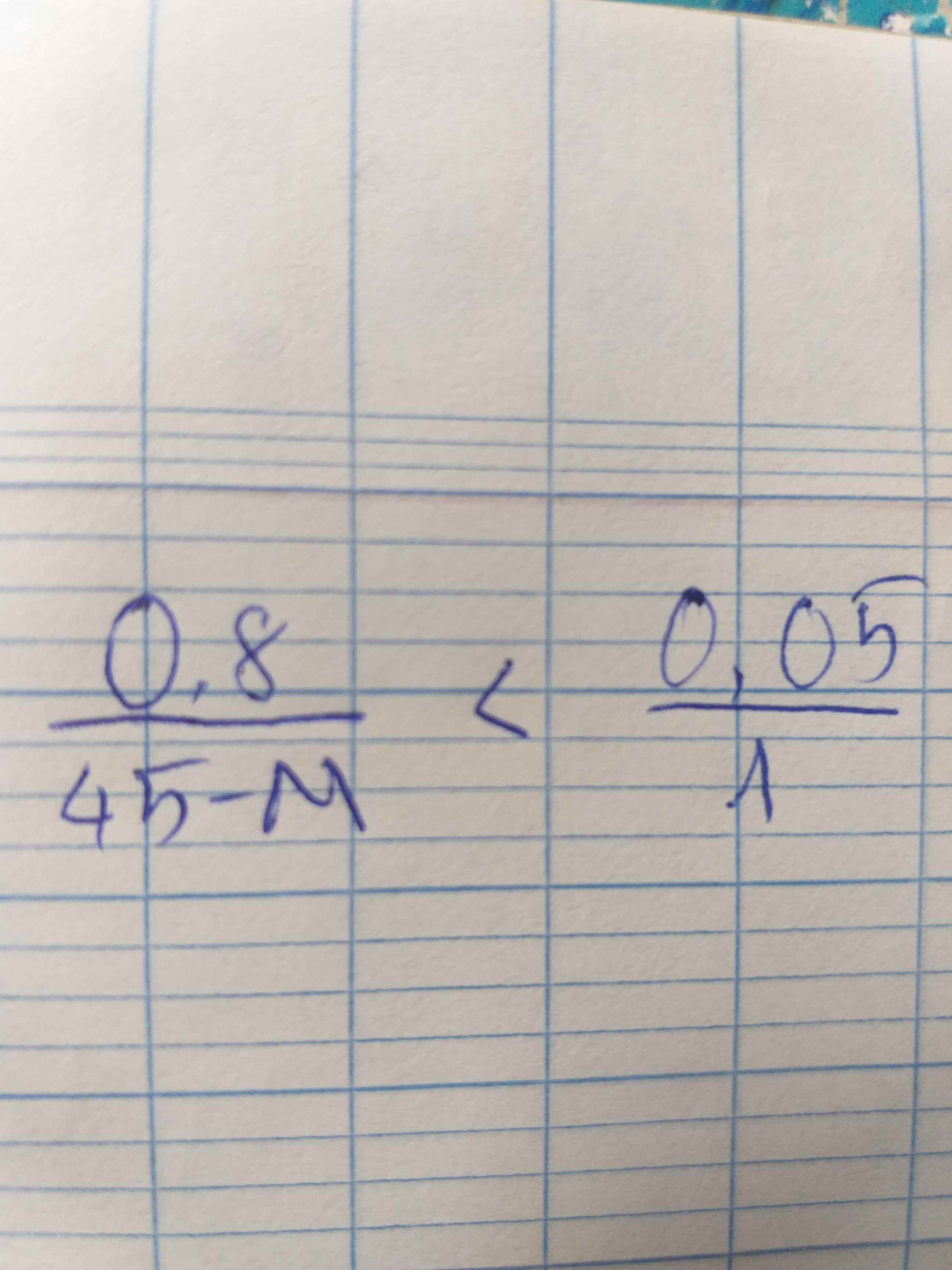

Mọi người giải dùm mình với ạ. Hoàn thành trước T3/14/9 nha :(((
Cám ơn mọi người nhìu <3
Mọi người giải dùm mình với!!!
1.Phân thích đa thức thành nhân tử
\(x^{20}+x+1\)
Ta có :
\(x^{20}+x+1\)
\(=\left(x^{20}-x^2\right)+\left(x^2+x+1\right)\)
Đặt \(x^2+x+1=A\)
\(\Rightarrow x^{20}+x+1=x^2\left(x^{18}-1\right)+A\)
\(=x^2\left(x^9+1\right)\left(x^9-1\right)+A\)
\(=\left(x^{11}+x^2\right)\left[\left(x^3\right)^3-1^3\right]+A\)
\(=\left(x^{11}+x^2\right)\left(x^6+1+x^3\right)\left(x^3-1\right)+A\)
\(=\left(x^{17}+x^{14}+x^{11}+x^8+x^5+x^2\right)\left(x-1\right)\left(x^2+x+1\right)+A\)
\(=A.\left(x^{18}-x^{17}+x^{15}-x^{14}+x^{12}-x^{11}+x^9-x^8+x^6-x^5+x^3-x^2\right)+A\)
\(=A.\left(x^{18}-x^{17}+x^{15}-x^{14}+x^{12}-x^{11}+x^9-x^8+x^6-x^5+x^3-x^2+1\right)\)
\(=\left(x^2+x+1\right)\left(x^{18}-x^{17}+x^{15}-x^{14}+x^{12}-x^{11}+x^9-x^8+x^6-x^5+x^3-x^2+1\right)\)
Đúng 0
Bình luận (0)
Mọi người ơi giải dùm e 2 câu này với ạ






