a) Ta có: AB^2 + AC^2 = 21^2 + 28^2 = 35^2 = BC^2 
Vậy Tam giác ABC vuông tại A (đl Pytago đảo) 
b) Ta có: Góc B + góc C = 90 độ (cmt câu a) 
Góc HAC + góc C = 90 độ (Tam giác HAC vuông tại H) 
=> Góc B = góc HAC 
Mà Góc AHB= Góc AHC = 90 độ (Đường cao AH) 
Vậy Tam giác HBA ~ tam giác HAC (góc - góc) 
c) 
Theo tính chất đường phân giác trong tam giác: 
MB/ AB = MC / AC 
<=> MB. AC = MC . AB 
<=> MB . AC = (35- MB) . AB 
<=> 35AB= MB.(AB+AC) 
<=> MB = 35AB/(AB+AC) = 35.21/(21+28) = 15 cm 
=> MC= 35 - 15 = 20 cm 
Vậy MB = 15 cm, MC 20 cm 
(Bạn tự vẽ hình và ghi giả thuyết kết luận nhé!)

Bạn ơi vẽ hình làm sao ạ

Ai giải giúp mình với. Mình cần gấp lắm

Thanks mina-san nhìu!!!

a/ Ta có: 21² + 28² = 35²

Vậy tam giác vuông tại B

sinA = \(\frac{28}{35}=\frac{4}{5}\)=> A

=> C = 180 - 90 - A

b/ H là gì thế

\(S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{21.28}{2}=294\left(cm^2\right)\)

Ta có:\(S_{ABC}=\dfrac{AB.AC}{2}\) mà ta lại có: \(S_{ABC}=\dfrac{AH.BC}{2}\)

\(\Rightarrow\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)

hình vẽ

câu a)

Trong ΔABC, ta có: AD là đường phân giác của (BAC)

Suy ra: 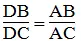 (tính chất đường phân giác)

Mà AB = 21 (cm); AC = 28 (cm)

Nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{21}{28}=\dfrac{3}{4}\)

Suy ra:

Suy ra: 

a)Ta có:`AB^2+AC^2=21^2+28^2=1225`

Mà `BC^2=1225`

Áp udnjg định lý ppytago đảo vào tam giác ABC có:`AB^2+AC^2=BC^2=1225`

`=>` tam giác ABC vuông

b)Vì BAC vuông tại A

`=>hat{BAC}=90^o`

`=>hat{HAB}=hat{HCA}=90^o-hat{HAC}`

Xét  tam giác HBA và tam giác HAC có"

`hat{HAB}=hat{HCA}`(CMT)

`hat{BHA}=hat{HAC}=90^o`

`=>`  tam giác HBA đồng dạng với tam giác HAC(gg)

c)Xét tam giác ACH và tam giác BAC ta có:

`hat{AHC}=hat{BAC}=90^o`

`hat{ACB}` chung

`=>DeltaACH~DeltaBAC(gg)`

`=>(AC)/(BH)=(BC)/(AC)`

`=>AC^2=BH.BC`.

d)Đường phân góc gì nhỉ?

a: ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot21\cdot28=294\left(cm^2\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)

mà \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)

nên \(AH\cdot BC=AB\cdot AC\)

b: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=21^2+28^2=1225\)

=>\(BC=\sqrt{1225}=35\left(cm\right)\)

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

 mà DB+DC=BC=35cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{35}{7}=5\)

=>\(DB=5\cdot3=15\left(cm\right);DC=4\cdot5=20\left(cm\right)\)

d,   tim AH=16,8cm do tam giác ABH dồng dạng với tam giác CBA các cạnh tuong ứng tỉ lệ

tinh CD tính chất dg pg \(\frac{CD}{DB}=\frac{AC}{AB}\)

tính chat day ti so bang nhau

\(\frac{CD}{DB+CD}=\frac{AC}{AB+AC}\)

thế số vao rồi tính suy ra CD=20, BD=15

pytago trong tam giác HAC tińh CH=22,4

suy ra DH=2,4

Diện tích tam giác AHD=1/2 *AH*DH=20,16

          Ban có thể tính laị so lieu