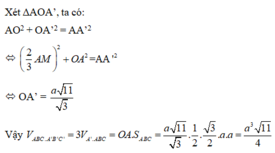Cho tam giác ABC đều cạnh a, trọng tâm G.Tính 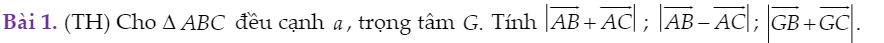
HL
Những câu hỏi liên quan
Cho tam giác đều ABC cạnh a, G là trọng tâm của tam giác. Khẳng định nào sau đây là đúng? A.
A
G
→
a
3
2
B.
A
G
→
+
...
Đọc tiếp
Cho tam giác đều ABC cạnh a, G là trọng tâm của tam giác. Khẳng định nào sau đây là đúng?
A. A G → = a 3 2
B. A G → + B G → = a
C. A G → + B G → + C G → = 0
D. A G → + B G → + C G → = 0 →
Nếu G là trong tâm tam giác ABC thì
G A → + G B → + G C → = 0 → ⇔ A G → + B G → + C G → = 0 → ⇔ A G → + B G → + C G → = 0 → = 0
Đáp án C
Đúng 0
Bình luận (0)
. Trong tam giác ABC các đường cao AE và BF cắt nhau tại H. Vậy điểm H
A. là trọng tâm của tam giác ABC.
B. là trực tâm của tam giác ABC.
C. cách đều ba đỉnh của tam giác ABC.
D. cách đều ba cạnh của tam giác ABC.
Xem chi tiết
cho tam giác ABC đều cạnh a trọng tâm G. Tích vô hướng của hai vecto BC*CG bằng
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng a, gọi G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng (ABC)bằng A.
a
6
9
B.
a
3
6
C.
a
6
6
D.
a
6...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng a, gọi G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng (ABC)bằng
A. a 6 9
B. a 3 6
C. a 6 6
D. a 6 12
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tam giác AGC quay quanh AG tạo thành một khối tròn xoay có thể tích là:
A
.
πa
3
3
36
B
.
πa
3
3
12
C
.
...
Đọc tiếp
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tam giác AGC quay quanh AG tạo thành một khối tròn xoay có thể tích là:
A . πa 3 3 36
B . πa 3 3 12
C . πa 3 3 24
D . πa 3 3 18
Gọi cho là ai trọng tâm của tam giác đều ABC cạnh 2 cm chứng minh cách đều ba cạnh của tam giác ABC từ đó tính khoảng cách từ G tới mỗi canh của 1 tam giác
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB a, AA 2a. Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A
.
a
3
11
4
B
.
a
3
11...
Đọc tiếp
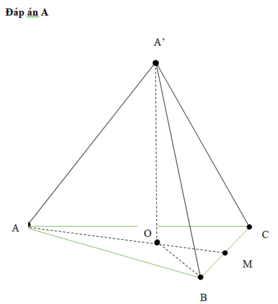
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB = a, AA'= 2a. Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A . a 3 11 4
B . a 3 11 12
C . a 3 47 8
D . 3 a 3 4
Đáp án A
Xét ∆AOA’, ta có:
AO2 + OA’2 = AA’2
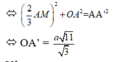
Vậy ![]()

Đúng 0
Bình luận (0)
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh ABa,AA2a . Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là: A.
a
3
11
4
B.
a
3
11
12
C. ...
Đọc tiếp
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB=a,AA'=2a . Hình chiếu của 'A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A. a 3 11 4
B. a 3 11 12
C. a 3 47 8
D. a 3 4
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, độ dài cạnh bên bằng
2
a
3
, hình chiếu của đỉnh A’ trên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ bằng A.
a
3
3
36
.
B. ...
Đọc tiếp
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, độ dài cạnh bên bằng 2 a 3 , hình chiếu của đỉnh A’ trên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ bằng
A. a 3 3 36 .
B. a 3 3 6 .
C. a 3 3 12 .
D. a 3 3 24 .