GB?

GP mới đúng chứ bẹn:v

Đó là điểm học tập đó bạn

tui ko b .

GP là điểm do giáo viên của hoc24 đánh giá.

SP là điểm do học sinh đánh giá lẫn nhau.

ko bik 

Vì E,H là trung điểm AB,GB nên EH là đtb tg ABG

Do đó EH//AG và \(EH=\dfrac{1}{2}AG\)

Vì F,K là trung điểm CA,CG nên FK là đtb tg AGC

Do đó FK//AG và \(FK=\dfrac{1}{2}AG\)

\(\Rightarrow FK//EH\text{ và }FK=EH\\ \Rightarrow DEHK\text{ là hình bình hành}\)

Để DEHK là hv

\(\Leftrightarrow\left\{{}\begin{matrix}EH\perp HK\\EK\perp HD\end{matrix}\right.\left(1\right)\)

Ta có HK là đtb tg BGC nên HK//BC 

Kết hợp \(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}AG\perp BC\left(EH//AG\right)\\BD\perp CE\end{matrix}\right.\)

Mà AG là trung tuyến nên ABC cân tại A

Vậy tam giác ABC cân tại A có trung tuyến BD,CE vuông góc với nhau thì DEHK là hình vuông

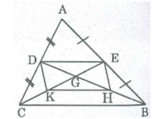
Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK

Mà DH = 2/3 BD; EK = 2/3 CE

Nên DH = EK ⇒ BD = CE

⇒ ∆ ABC cân tại A.

Vậy  ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.

a: Đề thiếu số đo rồi bạn

b: Xét ΔABC có

N,M lần lượt là trung điểm của AB,AC

=>NM là đường trung bình của ΔABC

=>NM//BC và \(NM=\dfrac{BC}{2}\)

Xét ΔGBC có

I,K lần lượt là trung điểm của GB,GC

=>IK là đường trung bình của ΔGBC

=>IK//BC và \(IK=\dfrac{BC}{2}\)

IK//BC

NM//BC

Do đó: IK//MN

\(IK=\dfrac{BC}{2}\)

\(MN=\dfrac{CB}{2}\)

Do đó: IK=MN

Xét tứ giác NMKI có

NM//KI

NM=KI

Do đó: NMKI là hình bình hành

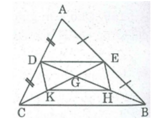
Nếu BD ⊥ CE ⇒ DH ⊥ EK

Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.

GP là điểm thành tích mà chỉ có được khi học 24h đánh tick cho bạn

GB or GP

a: Xét ΔABC có 

E là trung điểm của AB

F là trung điểm của AC

Do đó: EF là đường trung bình

=>EF//BC và EF=BC/2(1)

hay EFCB là hình thang

b: Xét ΔGBC có

K là trung điểm của GB

H là trung điểm của GC

Do đó: KH là đường trung bình

=>KH//BC và KH=BC/2(2)

Từ (1) và (2) suy ra EF=HK và EF=HK

hay EFKH là hình bình hành