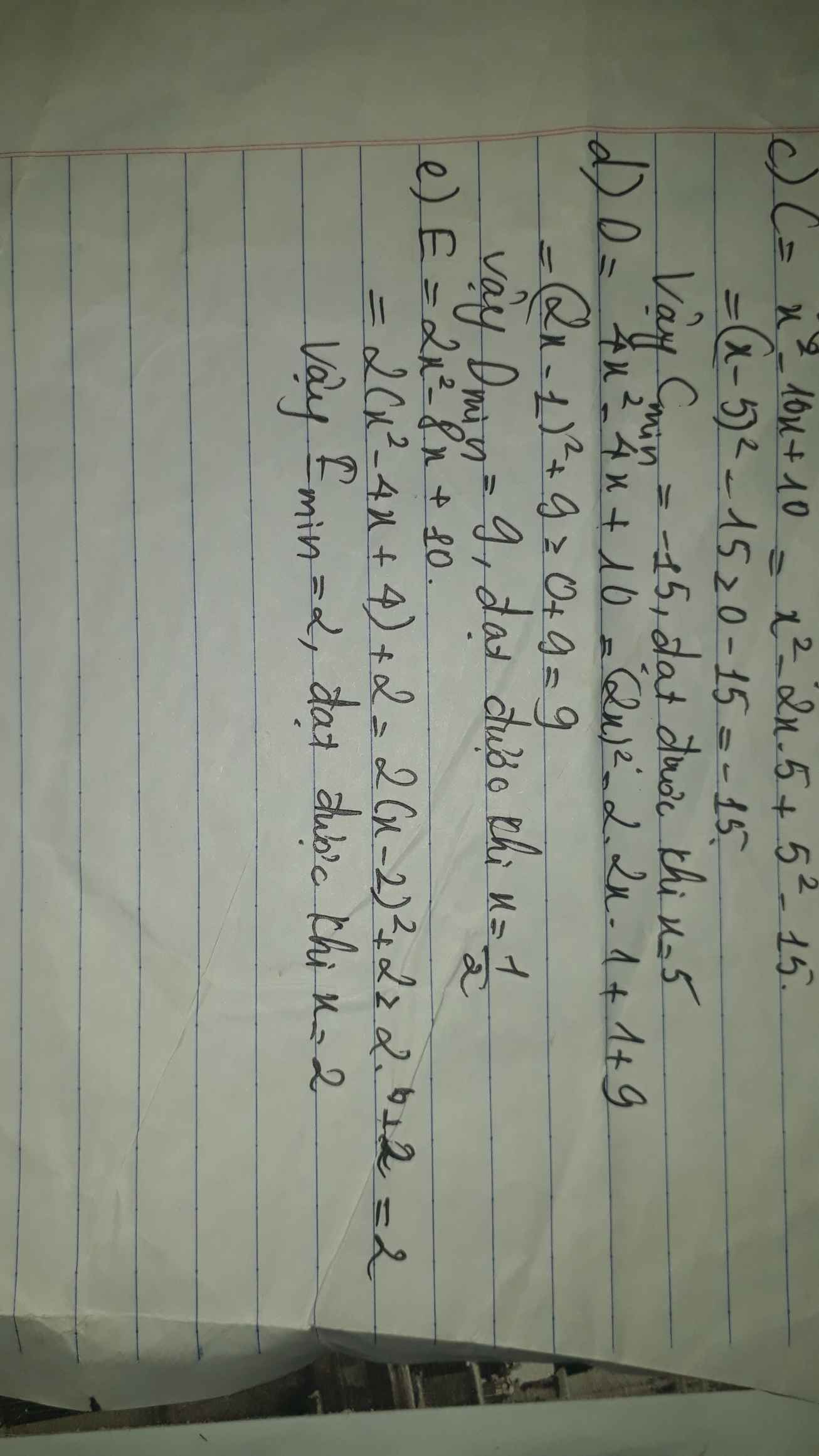a: Ta có: \(x\left(2x-3\right)-\left(2x-1\right)\left(x+5\right)=17\)

\(\Leftrightarrow2x^2-3x-2x^2-10x+x+5=17\)

\(\Leftrightarrow-12x=12\)

hay x=-1

\(A=-x^2+6x-10=-\left(x^2-6x+9\right)-1=-\left(x-3\right)^2-1\le-1\)

Vậy GTLN của A là -1 khi x = 3

\(B=-2x^2-4x-10=-2\left(x^2+2x+1\right)-8=-2\left(x+1\right)^2-8\le-8\)

Vậy GTLN của B là -8 khi x = -1

\(C=-2x^2+3x-10=-2\left(x^2-\frac{3}{2}x+\frac{9}{16}\right)-\frac{71}{8}=-2\left(x-\frac{3}{4}\right)^2-\frac{71}{8}\le-\frac{71}{8}\)

Vậy GTLN của C là \(-\frac{71}{8}\)khi x = \(\frac{3}{4}\)

\(D=-x^2-y^2+2x-4y-10\)

\(D=-\left(x^2-2x+1\right)-\left(y^2+4y+4\right)-5\)

\(D=-\left(x-1\right)^2-\left(y+2\right)^2-5\le-5\)

Vậy GTLN của D là -5 khi x = 1; y = -2

a) Ta có: \(A=x^2+4x+10\)

\(=x^2+4x+4+6\)

\(=\left(x+2\right)^2+6\ge6\forall x\)

Dấu '=' xảy ra khi x=-2

b) Ta có: \(B=x^2-2x+10\)

\(=x^2-2x+1+9\)

\(=\left(x-1\right)^2+9\ge9\forall x\)

Dấu '=' xảy ra khi x=2

c) Ta có: \(C=x^2-10x+10\)

\(=x^2-10x+25-15\)

\(=\left(x-5\right)^2-15\ge-15\forall x\)

Dấu '=' xảy ra khi x=5

d) Ta có: \(D=4x^2-4x+10\)

\(=4x^2-4x+1+9\)

\(=\left(2x-1\right)^2+9\ge9\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

\(a,A=-x^2+6x-10\)

\(=-x^2+6x-9-1\)

\(=-\left(x^2-6x+9\right)-1\)

\(=-\left(x-3\right)^2-1\)

Ta có: \(-\left(x-3\right)^2\le0\forall x\)

\(\Rightarrow-\left(x-3\right)^2-1\le-1\forall x\)

=> Max A =-1 tại \(-\left(x-3\right)^2=0\Rightarrow x=3\)

cn lại lm tg tự 

=.= hok tốt!!

x ( 2x - 3 ) + 2 = 2x² - 10

=> 2x² - 3x + 2 = 2x² - 10

=> -3x + 2 = -10

=> -3x = -12

=> x = 4

Vậy x = 4

a)\(=>2x=-10=>x=-5\)

b)\(=>-2x=-5=>x=\dfrac{-5}{-2}=\dfrac{5}{2}\)

c)\(4-x=0=>x=4-0=4\)

d)\(=>2x=-1=>x=-\dfrac{1}{2}\)

e)\(=>x^2=-2\)=> x ko tồn tại

f)\(=>x\left(2+1\right)=0=>3x=0=>x=0\)

2x²-10x+10=0

<=> x²-5x+5=0 ( chia cả 2 vế cho 2)

<=> \(x^2-2\times\frac{5}{2}x+\frac{25}{4}=\frac{5}{4}\)

<=> \(\left(x-\frac{5}{2}\right)^2=\frac{5}{4}\)

=> \(\orbr{\begin{cases}x=\sqrt{\frac{5}{4}}+\frac{5}{2}\\x=-\sqrt{\frac{5}{4}}+\frac{5}{2}\end{cases}}\)

\(x^3-2x^2+x-2=0\\ \Leftrightarrow x^2\left(x-2\right)+\left(x-2\right)=0\\ \Leftrightarrow\left(x^2+1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=2\end{matrix}\right.\\ Vậy:x=2\\ ---\\ 2x\left(3x-5\right)=10-6x\\ \Leftrightarrow6x^2-10x-10+6x=0\\ \Leftrightarrow6x^2-4x-10=0\\ \Leftrightarrow6x^2+6x-10x-10=0\\ \Leftrightarrow6x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(6x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}6x-10=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)

\(4-x=2\left(x-4\right)^2\\ \Leftrightarrow4-x=2\left(x^2-8x+16\right)\\ \Leftrightarrow2x^2-16x+32+x-4=0\\ \Leftrightarrow2x^2-15x+28=0\\ \Leftrightarrow2x^2-8x-7x+28=0\\ \Leftrightarrow2x\left(x-4\right)-7\left(x-4\right)=0\\ \Leftrightarrow\left(2x-7\right)\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=4\end{matrix}\right.\\ ---\\ 4-6x+x\left(3x-2\right)=0\\ \Leftrightarrow4-6x+3x^2-2x=0\\ \Leftrightarrow3x^2-8x+4=0\\ \Leftrightarrow3x^2-6x-2x+4=0\\ \Leftrightarrow3x\left(x-2\right)-2\left(x-2\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)