Cho \(\Delta ABC\), M là trung điểm của BC, \(\widehat{BAM}=30^o,\widehat{MAC}=15^o\). Tính góc BCA
H24
Những câu hỏi liên quan
Cho tam giác ABC , M là trung điểm của BC , góc BAM = 30 độ , góc MAC = 15 độ . Tính góc BCA ?
Lấy F là điểm đối xứng với B qua AM, gọi O là giao điểm của BF với AM
\(\Delta\)AOB vuông tại O có ^MAB = 300 (gt) nên ^ABO = 600
Lại có: AF = AB (theo tính chất đối xứng) nên \(\Delta\)AFB đều => ^AFB = 600
\(\Delta\)AFB đều có AO là đường cao nên cũng là trung tuyến => FO = OB
Có M là trung điểm của BC, O là trung điểm của FB nên OM là đường trung bình của \(\Delta\)BFC
=> OM // CF mà OM\(\perp\)FB nên BF\(\perp\)FC => \(\Delta\)BFC vuông tại F hay ^BFC = 900
Ta có: ^CFA = ^BFC + ^BFA = 900 + 600 = 1500
\(\Delta\)AFB đều có AO là đường cao nên cũng là phân giác => ^OAF = 300 => ^FAC = 150
Suy ra ^FCA = 150 hay \(\Delta\)CFA cân tại F => CF = AF
Mà AF = FB nên BF = FC do đó \(\Delta\)BFC vuông cân tại F => ^FBC = 450
=> ^ABC = ^CBF + ^FBA = 450 + 600 = 1050
Vậy ^BCA = 1800 - 1050 - (150 + 300) = 300
BCA\(=60\)nhớ cho mình
Cho tam giác ABC , M là trung điểm của BC , góc BAM = 30 độ , góc MAC = 15 độ . Tính góc BCA
Cho tam giác ABC có \(\widehat {BCA} = {60^o}\) và điểm M nằm trên cạnh BC sao cho \(\widehat {BAM} = {20^\circ },\widehat {AMC} = {80^\circ }({\rm{H}}.4.26).\) Tính số đo các góc AMB, ABC, BAC.
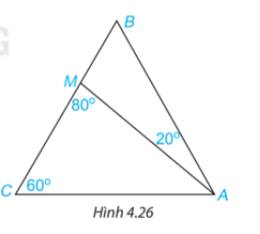
Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, M là trung điểm của BC, goác BAM = 30 độ , góc MAC = 15 độ . Tính góc BCA
Làm nhanh giúp mình nha!!!!!!!!!
Cho tam giác ABC. M là trung điểm của BC. Biết góc BAM= 30o, góc MAC= 15o. Tính góc BCA.
Cho Delta ABC. Gọi M là trung điểm của đoạn thẳng BC. Biết widehat{BAM}m^o; widehat{MAC}n^o.a, Tính widehat{BAC}b, Với giá trị nào của m^o và n^o thì AM là tia phân giác của widehat{BAC}?
Đọc tiếp
Cho \(\Delta ABC\). Gọi \(M\) là trung điểm của đoạn thẳng \(BC\). Biết \(\widehat{BAM}=m^o\); \(\widehat{MAC}=n^o\).
a, Tính \(\widehat{BAC}\)
b, Với giá trị nào của \(m^o\) và \(n^o\) thì \(AM\) là tia phân giác của \(\widehat{BAC}\)?
\(\Delta ABC,AB< AC,M\)là trung điểm của BC.So sánh \(\widehat{BAM}\)và\(\widehat{MAC}\)
Cho \(\Delta ABC\)có \(\widehat{B}=30^o;\widehat{C}=105^o\)và D là trung điểm của BC. Tính số đo của \(\widehat{BAD}\).
1. Cho △ABC có AB là cạnh lớn nhất, BC là cạnh nhỏ nhất. Chứng minh rằng widehat{C}60^o, widehat{A}le60^o.
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB AC. Chứng minh widehat{MAC} widehat{BAM}
b) Giả sử widehat{MAC} widehat{BAM}. Chứng minh AB AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho widehat{ADB} widehat{ADC}. Chứng minh BD DC
b) Cho △ABC vuông tại A. Chứng minh rằng AB^...
Đọc tiếp
1. Cho △ABC có AB là cạnh lớn nhất, BC là cạnh nhỏ nhất. Chứng minh rằng \(\widehat{C}>60^o\), \(\widehat{A}\le60^o\).
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB < AC. Chứng minh \(\widehat{MAC}< \widehat{BAM}\)
b) Giả sử \(\widehat{MAC}< \widehat{BAM}\). Chứng minh AB < AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC > BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho \(\widehat{ADB}< \widehat{ADC}\). Chứng minh BD > DC
b) Cho △ABC vuông tại A. Chứng minh rằng \(AB^{2017}+AC^{2017}< BC^{2017}\)
Bài 2 :
a, - Kéo dài AM tới điểm D sao cho AM = MD .
- Ta có : \(\widehat{M_1}\) và \(\widehat{M_2}\) đối đỉnh .
=> \(\widehat{M_1}\) = \(\widehat{M_2}\)
- Xét \(\Delta ABM\) và \(\Delta DCM\) có :
\(\left\{{}\begin{matrix}BM=CM\left(GT\right)\\\widehat{M_1}=\widehat{M_2}\left(cmt\right)\\AM=DM\left(GT\right)\end{matrix}\right.\)
=> \(\Delta ABM\) = \(\Delta DCM\) ( c - g - c )
=> \(\widehat{A_1}=\widehat{D_2}\) ( góc tương ứng )
=> \(AB=CD\) ( cạnh tương ứng )
Mà \(AB< AC\left(GT\right)\)
=> \(CD< AC\)
=> \(\widehat{MAC}< \widehat{ADC}\) ( quan hệ cạnh góc đối diện )
Mà \(\widehat{ADC}=\widehat{BAM}\) ( cmt )
=> \(\widehat{BAM}>\widehat{MAC}\) ( đpcm )
Nguyễn Ngọc Lộc Nguyễn Lê Phước ThịnhJeong Soo In?Amanda?Trần Quốc KhanhPhạm Lan HươngNatsu Dragneel 2005Trung NguyenNo choice teenPhạm Thị Diệu HuyềnTrên con đường thành công không có dấu chân của kẻ lười biếngNguyễn Thành TrươngAkai HarumaNguyễn Việt LâmHoàng YếntthNguyễn Văn Đạt




