Nêu bất đẳng thức AM-GM.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
CC
Những câu hỏi liên quan
giúp mình bài này với ( gợi ý : dùng bất đẳng thức AM GM)
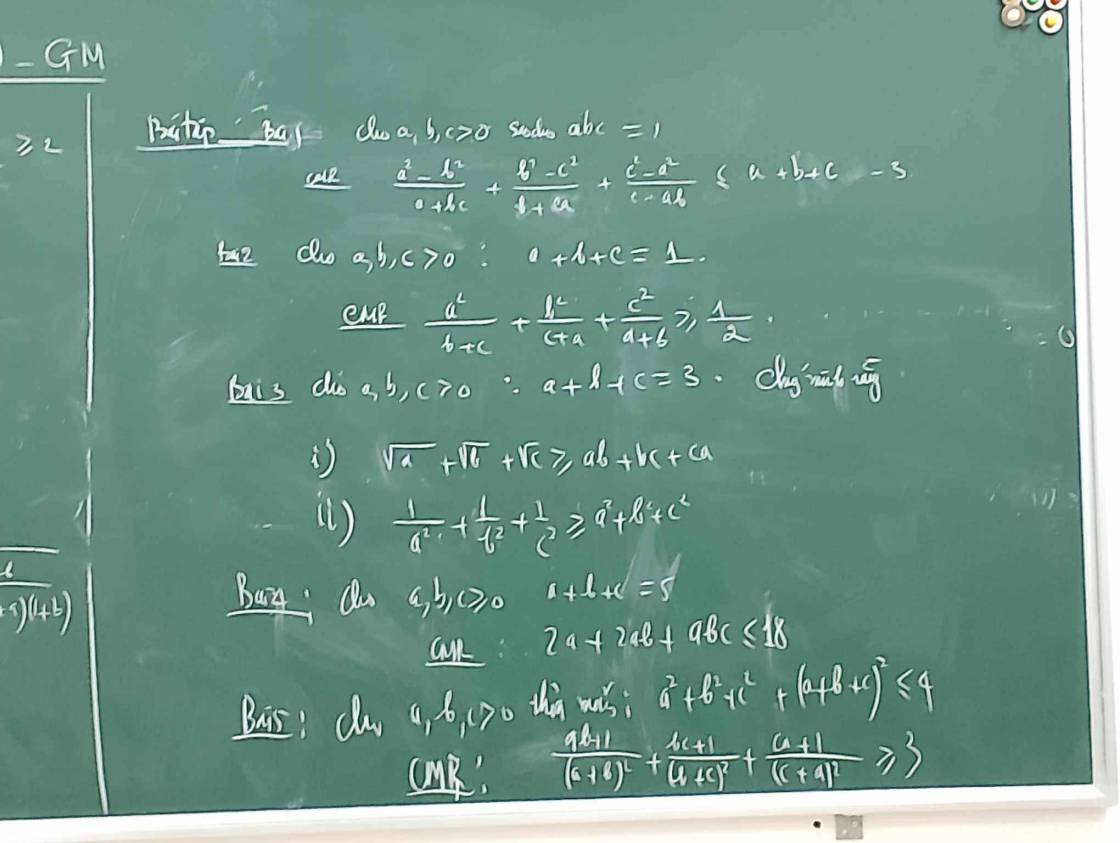
Bất đẳng thức Cauchy - Schwars
Bất đẳng thức AM - GM
Bất đẳng thức Bunhiacopxki
Bất đẳng thức Mincopxki
Cho tớ công thức của các BĐT trên , giúp với@Ace Legona
C-S với Bunhia là 1 và là 1 trg hợp của Holder dạng 2 số \(\left(a^2+b^2\right)\left(x^2+y^2\right)\ge\left(ax+by\right)^2\)
AM-GM ng` việt gọi là cô si dạng 2 số \(a^2+b^2\ge2ab\)
Mincopski dạng 2 số \(\sqrt{a^2+b^2}+\sqrt{x^2+y^2}\ge\sqrt{\left(a+x\right)^2+\left(b+y\right)^2}\)
Đúng 0
Bình luận (1)
* BĐT Cauchy - Schwars = BĐT Bunhiacopxki
- Thông thường :
( a2 + b2 )(c2 + d2 ) \(\ge\left(ac+bd\right)^2\)
Dấu "=" xảy ra tại : \(\dfrac{a}{c}=\dfrac{b}{d}\)
- Tổng quát với các bộ số : a1 , a2 , a3 , ... , an và : b1 , b2 , ... , bn
(a12 + a22 + ... + an2)(b12 + b22 + ... + bn2 ) \(\ge\left(a_1b_1+a_2b_2+...+a_nb_n\right)\)
Dấu "=" xảy ra tại : \(\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=...=\dfrac{a_n}{b_n}\)
* BĐT AM-GM
- trung bình nhân (2 số)
với a,b \(\ge0\) , ta luôn có : \(\dfrac{a+b}{2}\ge\sqrt{ab}\) . Dấu "=" xảy ra tại a=b
- Trung bình nhân ( n số )
Với x1 , x1 , x3 ,..., xn \(\ge0\)
Ta luôn có : \(\dfrac{x_1+x_2+...+x_n}{n}\ge\sqrt[n]{x_1x_2.....x_n}\)
Dấu "=" xảy ra khi x1 = x2 =...=xn
-Trung bình hệ số :
Với các bộ số : x1 , x1 , x3 ,..., xn \(\ge0\)và a1, a2 , a3 ,... , an ( a1 , a2 ,..., an) là c1ác hệ số
Ta có : \(\dfrac{a_1x_1+a_2x_2+...+a_nx_n}{a}\ge\sqrt[a]{x_1^{a_1}.x_2^{a_2}.....x_n^{a_n}}\)
Dấu "=" xảy ra khi x1 = x2 = xn
=================
Cái mincopxki t ko biết , ngoài ra còng có BĐT Cauchy - dạng engel => lên googl seach có
Đúng 0
Bình luận (0)
Cho mình hỏi bất đẳng thức AM-GM là gì vậy mọi người
Trong toán học, bất đẳng thức AM-GM là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Tên gọi đúng của bất đẳng thức này là bất đẳng thức AM-GM. Bất đẳng thức AM-GM là một bất đẳng thức cơ bản kinh điển quan trọng nhất của toán học sơ cấp, vì nó đã có khá nhiều cách chứng minh được đưa ra, hàng chục mở rộng, hàng chục kết quả chặt hơn đăng trên các diễn đàn toán học. Phần này tôi xin giới thiệu một kết quả chặt hơn bất đẳng thức AM-GM khác được suy ra từ chính cách chứng minh mới bất đẳng thức AM-GM (Cauchy - Cô-si).
# Aeri #
Mọi người cho mình biết bất đẳng thức AM-GM được ko?
mình copy trên google nè:Bất đẳng thức này ở VN gọi là bđt Cô-si (Cauchy) còn ở Mỹ gọi như trong tựa bài, hay gọi tắt là AM-GM inequality (arithmetic mean - geometric mean)
Đúng 0
Bình luận (0)
cho mình hỏi về bất đẳng thức AM-Gm, Cô-si và Cauchy nó có phải là 1 không
Xem thêm câu trả lời
Mong các bạn giúp ạ
Rất cần gấp để thi chuyên
Xét các số thực dương x+y≤1 cmr
X+y + 1/x +1/y ≥ 5
Nghe nói áp dụng bất đẳng thức am gm
Đặt \(P=x+y+\frac{1}{x}+\frac{1}{y}\)
\(=x+y+\frac{1}{4x}+\frac{3}{4x}+\frac{1}{4y}+\frac{3}{4y}\)
\(=\left(x+\frac{1}{4x}\right)+\left(y+\frac{1}{4y}\right)+\left(\frac{3}{4x}+\frac{3}{4y}\right)\)
Áp dụng bđt AM-GM cho 2 số thực dương x,y ta được:
\(x+\frac{1}{4x}\ge2\sqrt{x.\frac{1}{4x}}=1\left(1\right)\)
\(y+\frac{1}{4y}\ge2\sqrt{y.\frac{1}{4y}}=1\left(2\right)\)
\(\frac{3}{4x}+\frac{3}{4y}\ge2\sqrt{\frac{3}{4x}.\frac{3}{4y}}=\frac{3}{2\sqrt{xy}}\left(3\right)\)
Áp dụng bđt AM-GM ta có:
\(\sqrt{xy}\le\frac{x+y}{2}=\frac{1}{2}\left(4\right)\)
Thay (4) vào (3) ta có \(\frac{3}{4x}+\frac{3}{4y}\ge3\left(5\right)\)
(1)+(2)+(5) ta được: \(P\ge3\)
Dấu"="Xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Nêu bất đẳng thức tam giác
Trong toán học, bất đẳng thức tam giác là một định lý phát biểu rằng trong một tam giác chiều dài của một cạnh phải nhỏ hơn tổng, nhưng lớn hơn hiệu của hai cạnh còn lại.
Đúng 1
Bình luận (1)
Trong chương trình lớp 7 thì có bất đẳng thức là:
Trong tam giác, tổng độ dài 2 cạnh bao giờ cũng lớn hơn cạnh còn lại
Đúng 1
Bình luận (0)
Nêu các dạng bất đẳng thức đã học
VÀ NÊU VÍ DỤ
Các bất đẳng thức nổi tiếng
Bất đẳng thức Bunyakovsky.Bất đẳng thức Azuma.Bất đẳng thức Bernoulli.Bất đẳng thức Boole.Bất đẳng thức Cauchy-Schwarz.Bất đẳng thức cộng Chebyshev.Bất đẳng thức Chernoff.Bất đẳng thức Cramer-Rao:333Tôi đã học :
-bất đảng thức cô-si
-bất đảng thức bunyakovsky
về phần ví dụ thì tui chịu nha
Quên hết rùi
Nêu một bài toán về bất đẳng thức cô si




