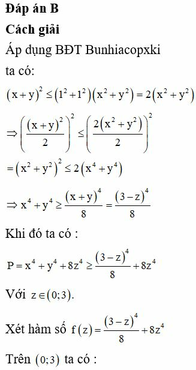Cho các số nguyên dương a,b,x,y thỏa mãn các đẳng thức: a+b=x+y, ab+a=xy.Chứng tỏ x=y
DH
Những câu hỏi liên quan
Cho các số nguyên dương a,b,x,y thỏa mãn các đẳng thức: a+b=x+y, ab+a=xy.Chứng tỏ x=y
Bạn xem lại đề bài. Với $a=2; b=5; x=3; y=4$ thì những đẳng thức đã cho đều thỏa mãn nhưng $x\neq y$
Đúng 0
Bình luận (1)
Cho các số nguyên dương a,b,x,y thỏa mãn các đẳng thức: a+b=x+y, ab+a=xy.Chứng tỏ x=y
Cho các số nguyên dương a,b,x,y thỏa mãn các đẳng thức: a+b=x+y ; a.b-a=x.y. Chứng tỏ rằng x khác y
a)Tìm các số nguyên dương x, y thỏa mãn x+3 chia hết cho y, y+3 chia hết cho x
b)Tìm các số nguyên dương x, y thỏa mãn xy+x+y+2 chia hết cho cả x và y.
Cho các số thực dương x, y, z và thỏa mãn x + y + z 3. Biểu thức
P
x
4
+
y
4
+
8
z
4
đạt GTNN bằng
a
b
, trong đó a, b là các số tự nhiên dương,
a
b
là phân số tối giản. Tính a - b A. 234. B. 523. C. 235. D. 525.
Đọc tiếp
Cho các số thực dương x, y, z và thỏa mãn x + y + z = 3. Biểu thức P = x 4 + y 4 + 8 z 4 đạt GTNN bằng a b , trong đó a, b là các số tự nhiên dương, a b là phân số tối giản. Tính a - b
A. 234.
B. 523.
C. 235.
D. 525.
cho x;y;z là các số nguyên dương và x+y+z là số lẻ, các số thực a,b,c thỏa mãn: a-b/x=b-c/y=a-c/z.cmr: a=b=c
a-b+b-x-a+c/x+y-z=0/x+y-z=0
suy ra a-b=0 suy ra a=b
b-c=0 suy ra b=c
Đúng 0
Bình luận (0)
Câu 1: xy + x - y = 4
<=> (xy + x) - (y+ 1) = 3
<=> x(y+1) - (y + 1) = 3 <=> (y + 1) (x - 1) = 3
Theo bài ra cần tìm các số nguyên dương x, y =>
Xét các trường hợp y + 1 nguyên dương và x -1 nguyên dương.
Mà 3 = 1 x 3 => Chỉ có thể xảy ra các trường hợp sau:
* TH1: y + 1 = 1; x - 1 = 3 => y = 0; x = 4 (loại vì y = 0)
* TH2: y + 1 = 3; x -1 = 1 => y = 2; x = 2 (t/m)
Vậy x = y = 2.
Câu 2: Ta có: (a - b)/x = (b-c)/y = (c-a)/z
=(a-b + b -c + c - a) (x + y + z) = 0 Vì x; y
; z nguyên dương => a-b =0; b - c = 0; c- a =0 => a = b = c
Đúng 0
Bình luận (0)
Cho a,b,c,x,y,z là các số nguyên dương và ba số a,b,c khác 1 thỏa mãn a^x=bc;b^y=ca;c^z=ab. chứng minh : x+y+z+2=xyz! Giup mk vs
cho x,y,z là các số nguyên dương và x +y+z là số lẻ, các số thực a,b,c thỏa mãn (a-b)/x=(b-c)/y= (a-c)/z chứng minh rằng a= b= c
Cho x,y,z là các số nguyên tố khác 2 và các số thực a,b,c thỏa mãn dãy tỉ số bằng nhau a-b/x=b-c/y=a-c/z.CMR a=b=c
Đúng 0
Bình luận (0)
Dễ thế mà chẳng ai làm được..
a) Tìm cặp số x,y nguyên dương thỏa mãn \(x^2+y^2\left(x-y+1\right)-\left(x-1\right)y=22\)
b) Tìm các cặp số x,y,z nguyên dương thỏa mãn \(\dfrac{xy+yz+zx}{x+y+z}=4\)