Trong mặt phẳng Oxy phép quay tâm K, góc 60 o biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:
A. (0;0)
B. (0;-√3)
C. (0;1-√3)
D. (√2;0)
Trong mặt phẳng Oxy phép quay tâm K, góc 60 o biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:
A. (0;0)
B. (0;-√3)
C. (0;1-√3)
D. (√2;0)
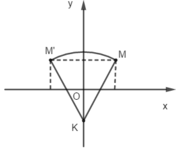
Tam giác đều KMM’ có cạnh MM’ = 2 nên đường cao bằng √3.
Suy ra OK = √3-1 ⇒ K(0; 1-√3)
Nhận xét. Phép quay có góc quay bằng ±600 thì tam giác tạo bởi tâm quay, điểm M và ảnh M’ của nó luôn tạo thành một tam giác đều.
Đáp án C
Trong mặt phẳng tọa độ Oxy cho điểm M(1;0). Phép quay tâm O góc quay 45 o biến M thành M’ có tọa độ
A. 2 ; 2
B. 2 2 ; - 2 2
C. 2 ; - 2
D. 2 2 ; 2 2
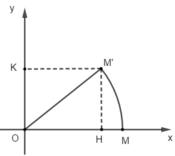
Ta có OM’ = OM = 1; tứ giác OHM’K là hình vuông đường chéo bằng 1 suy ra cạnh bằng (√2)/2.
Chọn đáp án D
Trong mặt phẳng tọa độ Oxy, phép quay tâm O góc quay 90 ° biến điểm M - 1 ; 2 thành điểm M'. Tọa độ điểm M' là
A. M ' 2 ; 1
B. M ' 2 ; - 1
C. M ' - 2 ; - 1
D. M ' - 2 ; 1
Trong mặt phẳng Oxy, thực hiện liên tiếp phép quay tâm O góc quay - 45 o và phép đối xứng tâm O thì điểm M(1;1) biến thành điểm M’’ có tọa độ là:
A. (-1;0)
B. (√2;0)
C. (√2;-√2)
D. (-√2;0)
+) Phép quay tâm O góc quay − 45 ° biến điểm M(x; y) thành điểm M’(x’;y’) với biểu thức tọa độ là:
Với M(1; 1) suy ra tọa độ điểm M’ là x ' = x cos − 45 ° − y sin − 45 ° y ' = x sin − 45 ° + y cos − 45 ° ⇔ x ' = 2 2 x + 2 2 y y ' = − 2 2 x + 2 2 y
+) Phép đối xứng tâm O biến điểm M’ thành M’’ x ' = 2 2 .1 + 2 2 .1 = 2 y ' = − 2 2 .1 + 2 2 .1 = 0 ⇒ M ' 2 ; 0
Suy ra tọa độ M ' ' − 2 ; 0
Đáp án D
Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng tâm O và phép quay tâm O góc quay 90 o biến đường thẳng y = x + 1 thành đường thẳng
A. x - y - 1 = 0
B. -x + y - 1 = 0
C. x + y + 1 = 0
D. x + y - 1 = 0
Đáp án D
+) Lấy điểm M(x; y) thuộc đường thẳng d có phương trình y = x + 1
Gọi M’(x’; y’) là ảnh của M qua phép đối xứng tâm O
Khi đó ta có: x ' = − x y ' = − y
Suy ra M’(-x; -y)
Gọi M’’ là ảnh của M’ qua phép quay tâm O góc 90 °
Khi đó tọa độ của M’’ là: x ' ' = − − y = y y ' ' = − x ⇔ x = − y ' ' y = x ' '
Thay vào phương trình d ta được: x’’ = -y’’ + 1 hay x’’ + y’’ - 1 = 0
Hay x + y - 1 = 0
Đáp án D
Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng trục Oy và phép quay tâm O góc quay 90 ° biến điểm M (1;1) thành điểm M''. Tọa độ M'' là:
A. - 1 ; 1 .
B. - 1 ; - 1 .
C. 1 ; - 1 .
D. - 2 ; - 2
Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng trục Oy và phép quay tâm O góc quay 90 o biến điểm M(1;1) thành điểm M’’. Tọa độ M’’ là:
A. (-1;1)
B. (-1;-1)
C.(1;-1)
D. (-√2;-√2)
Đáp án B
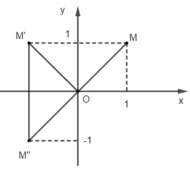
+ Phép đối xứng trục Oy biến điểm M(1; 1) thành điểm M’ có tọa độ là: x ' = − x = − 1 y ' = y = 1
Suy ra M’(-1; 1)
+ Phép quay tâm O góc quay biến điểm M’(-1; 1) thành điểm M’’ có tọa độ là: x ' ' = − y ' = − 1 y ' ' = x ' = − 1
Do đó M’’(-1; -1).
Đáp án B
Trong mặt phẳng Oxy, phép quay tâm O, góc quay 90◦ biến điểm M(−3; 5) thành điểm có tọa độ là
A. (3; 4). B. (−5; −3). C. (5; −3). D. (−3; −5).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x - 1 2 + y - 2 2 = 4 . Phép đồng dạng thực hiện bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k= - 2 và phép quay tâm O góc quay 180 ∘ , khi đó đường tròn (C) sẽ biến thành đường tròn nào sau đây
A. x 2 + y 2 - 4 x - 8 y - 2 = 0
B. x 2 + y 2 + 4 x + 8 y + 2 = 0
C. x + 2 2 + y + 4 2 = 16
D. x - 2 2 + y - 4 2 = 16
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x - 3 2 + y 2 = 4 . Phép quay tâm O(0;0) góc quay 90 o biến (C) thành (C’) có phương trình:
A. x 2 + y 2 - 6 x + 5 = 0
B. x 2 + y 2 - 6 y + 6 = 0
C. x 2 + y 2 + 6 x - 6 = 0
D. x 2 + y 2 - 6 y + 5 = 0
Phép quay tâm O(0; 0) góc quay 90 o biến tâm I(3; 0) của (C) thành tâm I’(0; 3) của (C’), bán kính không thay đổi. phương trình (C’) là x 2 + y - 3 2 = 4 ⇒ x 2 + y 2 - 6 y + 5 = 0
Đáp án D