Giúp mình vớiiii
VV
Những câu hỏi liên quan
Giúp mình vớiiii
Tổng đã cho là tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\dfrac{1}{2}}=2\)
Đúng 0
Bình luận (0)
Giúp mình vớiiii
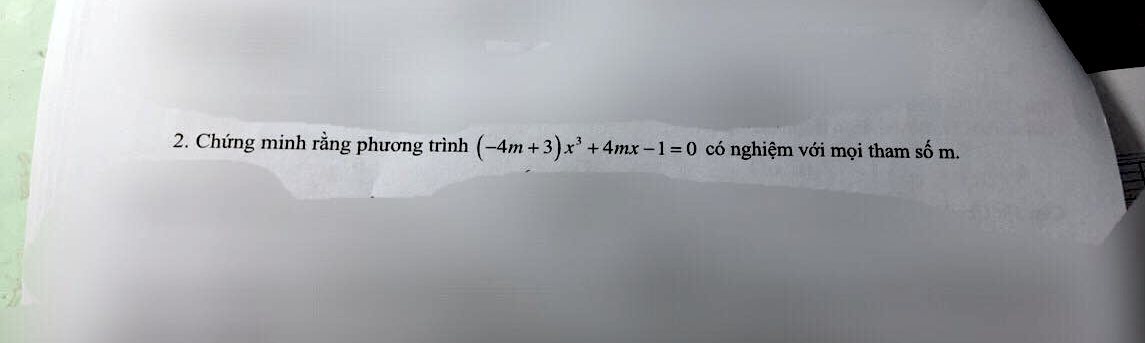
Lời giải:
Xét hàm $f(x)=(-4m+3)x^3+4mx-1$ liên tục trên $R$
$f(1)=-4m+3+4m-1=2>0$
$f(-1)=4m-3-4m-1=-4<0$
$\Rightarrow f(1)f(-1)<0$
Do đó pt $f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(-1;1)$ với mọi $m$ (đpcm)
Đúng 1
Bình luận (0)
Giúp mình vớiiii
Olm chào em. Em gặp phải chuyện gì vậy, hay em cần giải bài tập nào? Em hãy yêu cầu cụ thể để được trợ giúp nhé
Đúng 0
Bình luận (0)
mình cần gấp, giúp mình nhanh vớiiii
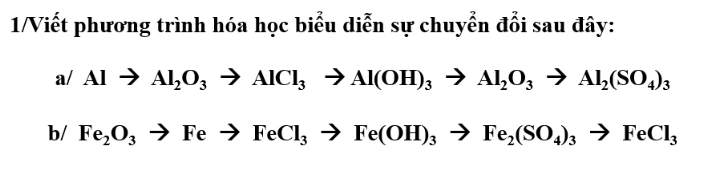
giải giúp mình vớiiii
Quy ước :
A : quy định tính trạng thân cao.
a : quy định tính trạng thân thấp.
B : quy định tính trạng quả đỏ.
b : quy định tính trạng quả vàng.
Cho cà chua thân cao, quả đỏ thuần chủng lai với cà chua thân thấp, quả vàng thu được F1.
=> P có KG là : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng).
* Sơ đồ lai :
P : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng)
G : AB ab
F1 : AaBb ( 100 % thân cao quả đỏ ).
Đúng 0
Bình luận (0)
Quy ước :
A : quy định tính trạng thân cao.
a : quy định tính trạng thân thấp.
B : quy định tính trạng quả đỏ.
b : quy định tính trạng quả vàng.
Cho cà chua thân cao, quả đỏ thuần chủng lai với cà chua thân thấp, quả vàng thu được F1.
=> P có KG là : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng).
* Sơ đồ lai :
P : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng)
G : AB ab
F1 : AaBb ( 100 % thân cao quả đỏ ).
Đúng 1
Bình luận (0)
giúp mình nhanh nhanh vớiiii
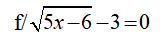
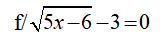
\(\sqrt{\text{5x - 6}}\) = 3
5x - 6 = 9
5x = 15
x =3
Đúng 4
Bình luận (0)
ĐKXĐ: \(x\ge\dfrac{6}{5}\)
\(\sqrt{5x-6}-3=0\)
\(\Leftrightarrow\sqrt{5x-6}=3\)
\(\Leftrightarrow\left|5x-6\right|=9\)
\(\Rightarrow5x-6=9\)
\(\Leftrightarrow x=3\) (TM)
Đúng 4
Bình luận (2)
Xem thêm câu trả lời
Mấy bạn giúp mình vớiiii
giải gấp giúp mình vớiiii
giải gấp giúp mình bài này vớiiii, mình cảm ơn

\(b,\text{PT hoành độ giao điểm: }3x-1=x+2\\ \Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow y=\dfrac{7}{2}\Leftrightarrow A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\\ \text{Vậy }A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\text{ là giao 2 đths}\\ c,\left(D_2\right)\text{//}\left(D\right);B\left(1;0\right)\in\left(D_2\right)\Leftrightarrow\left\{{}\begin{matrix}a+b=0\\a=3;b\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-3\end{matrix}\right.\\ \Leftrightarrow\left(D_2\right):y=3x-3\)
Đúng 0
Bình luận (0)




