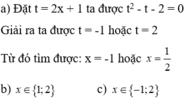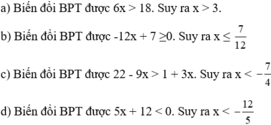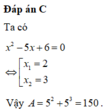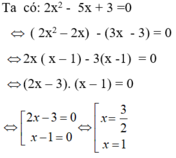giải phương trình tích sau:
(x2 + 5x2) - 2 (x2 + 5x) - 24 = 0
H24
Những câu hỏi liên quan
Giải các phương trình sau:a)
2
x
+
1
2
−
2
x
−
1
2
;
b)
x
2
−
3
x
2
+
5
x...
Đọc tiếp
Giải các phương trình sau:
a) 2 x + 1 2 − 2 x − 1 = 2 ;
b) x 2 − 3 x 2 + 5 x 2 − 3 x + 6 = 0 ;
c) x 2 − x − 1 x 2 − x − 2 = 0 .
Giải các bất phương trình sau:a)
2
x
−
7
11
−
4
x
;
b)
x
−
2
2
−
x
2
−
8
x
+
3
≥
0
;
c)
2
3
−
3...
Đọc tiếp
Giải các bất phương trình sau:
a) 2 x − 7 > 11 − 4 x ; b) x − 2 2 − x 2 − 8 x + 3 ≥ 0 ;
c) 2 3 − 3 x − 6 2 > 1 + 3 x 6 ; d) x − 5 x + 1 + 4 x + 3 < − 5 x 2
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 2 x 2 + 5x + 3 = 0
2 x 2 + 5x + 3 = 0 ⇔ 2 x 2 + 2x + 3x + 3 = 0
⇔ 2x(x + 1) + 3(x + 1) = 0 ⇔ (2x + 3)(x + 1) = 0
⇔ 2x + 3 = 0 hoặc x + 1 = 0
2x + 3 = 0 ⇔ x = -1,5
x + 1 = 0 ⇔ x = -1
Vậy phương trình có nghiệm x = -1,5 hoặc x = -1
Đúng 0
Bình luận (0)
Đối với mỗi phương trình sau, kí hiệu x1 và x2 là hai nghiệm (nếu có). Không giải phương trình, hãy điền vào những chỗ trống (...):
5x2 – x – 35 = 0;
Δ = …; x1 + x2 = …; x1.x2 = …;
5x2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b2 – 4ac = (-1)2 – 4.5.(-35) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x1 + x2 = -b/a = 1/5
x1.x2 = c/a = -35/5 = -7.
Đúng 0
Bình luận (0)
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
x
2
-
5
x
+
6
0
Tính giá trị của
A
5
x
1
+
5
x
2
A.
A...
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình x 2 - 5 x + 6 = 0 Tính giá trị của A = 5 x 1 + 5 x 2
A. A = 125
B. A = 3125
C. A = 150
D. A = 15625
Giải bất phương trình sau: (x2 + 1)(x2 + 2)(x2 + 3)(x2 + 4) - 24 > 0
\(\Leftrightarrow\left(x^4+5x^2+6\right)\left(x^4+5x^2+4\right)-24\)
Đặt \(x^4+5x^2+6=t\)
\(t\left(t-2\right)-24=t^2-2t-24\)
\(\Leftrightarrow t^2-2t+1-25=\left(t-1\right)^2-5^2=\left(t-6\right)\left(t+4\right)>0\)
TH1 : \(\left\{{}\begin{matrix}t-6>0\\t+4>0\end{matrix}\right.\Leftrightarrow t>6\)
TH2 : \(\left\{{}\begin{matrix}t-6< 0\\t+4< 0\end{matrix}\right.\)<=> t < -4
Theo cách đặt \(x^4+5x^2+6>6\Leftrightarrow x^2\left(x^2+5\right)>0\)* luôn đúng *
\(x^4+5x^2+6< -4\Leftrightarrow x^4+5x^2+10< 0\)
\(\Leftrightarrow x^4+\dfrac{2.5}{2}x^2+\dfrac{25}{4}+\dfrac{15}{4}< 0\Leftrightarrow\left(x^2+\dfrac{5}{2}\right)^2+\dfrac{15}{4}< 0\)( vô lí )
Đúng 0
Bình luận (1)
Đối với mỗi phương trình sau, kí hiệu x1 và x2 là hai nghiệm (nếu có). Không giải phương trình, hãy điền vào những chỗ trống (...):
a
)
2
x
2
–
17
x
+
1
0
;
Δ
…
;
x
1
+
x
2...
Đọc tiếp
Đối với mỗi phương trình sau, kí hiệu x1 và x2 là hai nghiệm (nếu có). Không giải phương trình, hãy điền vào những chỗ trống (...):
a ) 2 x 2 – 17 x + 1 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ; b ) 5 x 2 – x – 35 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ; c ) 8 x 2 – x + 1 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ; d ) 25 x 2 + 10 x + 1 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ;
a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25
Đúng 0
Bình luận (0)
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: – x 2 + 5x – 6 = 0
– x 2 + 5x – 6 = 0 ⇔ - x 2 + 2x + 3x – 6 = 0
⇔ - x(x – 2) + 3(x – 2) = 0 ⇔ (x – 2)(3 – x) = 0
⇔ x – 2 = 0 hoặc 3 – x = 0
x – 2 = 0 ⇔ x = 2
3 – x = 0 ⇔ x = 3
Vậy phương trình có nghiệm x = 2 hoặc x = 3.
Đúng 0
Bình luận (0)
Giải phương trình sau: 2
x
2
- 5x + 3 0 A.
x
-
3
2
h
o
ặ
c
x
1
B.
x
3
2
h
o
ặ
c
x
-
1
C.
x
-...
Đọc tiếp
Giải phương trình sau: 2 x 2 - 5x + 3 = 0
A. x = - 3 2 h o ặ c x = 1
B. x = 3 2 h o ặ c x = - 1
C. x = - 3 2 h o ặ c x = - 1
D. x = 3 2 h o ặ c x = 1
Cho phương trình 5x2 - 2x - 7 = 0. a) Không giải phương trình, tính tổng và tích hai nghiệm. b) Tính giá trị của biểu thức A = x12 + x22 – x1. x2
a. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{5}\\x_1x_2=-\dfrac{7}{5}\end{matrix}\right.\)
b.
\(A=x_1^2+x_2^2-x_1x_2=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(\dfrac{2}{5}\right)^2-3\left(-\dfrac{7}{5}\right)=\dfrac{109}{25}\)
Đúng 1
Bình luận (0)