cho 3 số cách đều nhau : ab;ba;acb.hãy tìm 3 số đó.
VT
Những câu hỏi liên quan
cho 3 số cách đều nhau : ab;ba;acb.hãy tìm 3 số đó.
cho 3 số cách đều nhau :ab ;ba ;abc .tìm 3 số đó.
98,99,100 đúng ko?ko đúng thì là hôm qua,hôm nay,ngày mai.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 3 số cách đều nhau: ab ; ba ; acb .Hãy tìm 3 số đó.
tìm 3 số cách đều nhau ab; ba ; acb
3 bạn Bắc, Trung, Nam cùng chơi 1 trò chơi. Bắc đếm các số tăng dần cách đều 10 bắt đầu từ 7. Trung đếm các số giảm dần cách đều 5 bắt đầu từ 3007. Nam đếm các số tăng dần cách đều 9 bắt đầu từ 207. 3 bạn cùng đếm một lúc cho đến khi cả 3 nói ra 1 số thì dừng lại. Biết rằng số các bạn nói ra đều bằng nhau, tìm số đó
Có thể nhận thấy 3 bạn cùng đếm cho đến khi dừng lại cùng lúc, như vậy số lần đếm của 3 bạn là như nhau. Khi dừng lại 3 bạn cùng dừng ở 1 số. Như vậy nếu gọi số lần đếm là x thì ta có: 7+ 10×x = 207+9×x . Giải phép toán này ta tìm được số lần đếm của 3 bạn là 200. Vậy số cần tìm là: 7+10×200=2007.
Đúng 0
Bình luận (0)
3 bạn Bắc, Trung, Nam cùng chơi 1 trò chơi. Bắc đếm các số tăng dần cách đều 10 bắt đầu từ 7. Trung đếm các số giảm dần cách đều 5 bắt đầu từ 3007. Nam đếm các số tăng dần cách đều 9 bắt đầu từ 207. 3 bạn cùng đếm một lúc cho đến khi cả 3 nói ra 1 số thì dừng lại. Biết rằng số các bạn nói ra đều bằng nhau, tìm số đó
Có thể nhận thấy 3 bạn cùng đếm cho đến khi dừng lại cùng lúc, như vậy số lần đếm của 3 bạn là như nhau.
Khi dừng lại 3 bạn cùng dừng ở 1 số.
Như vậy nếu gọi số lần đếm là x thì ta có:
7+ 10×x = 207+9×x .
Giải phép toán này ta tìm được số lần đếm của 3 bạn là 200.
Vậy số cần tìm là: 7+10×200=2007.
Đúng 0
Bình luận (0)
cho đường tròn tâm O và 2 dây AB, CD bằng nhau và cắt nhau tại I, sao cho D thuộc cung nhỏ AB. chứng minh điểm O cách đều AD, BC
Cho đường tròn tâm O, 2 dây AB và CD bằng nhau và cắt nhau tại I sao cho D thuộc cung nhỏ AB. Chứng minh điểm O cách đều AD và CB.
Cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.
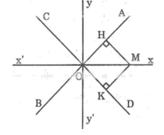
* Xét điểm M nằm trong góc AOD
Kẻ MH ⊥ OA, MK ⊥ OD
Xét hai tam giác MHO và MKO:
∠(MHO) = ∠(MKO) = 90o
MH = MK
OM cạnh huyền chung
Suy ra: ΔMHO = ΔMKO
(cạnh huyền - cạnh góc vuông)
Suy ra: ∠(MOH) = ∠(MOK)(2 góc tương ứng)
Hay OM là tia phân giác của ∠(AOD).
* Ngược lại, M nằm trên tia phân giác của ∠(AOD)
Xét hai tam giác vuông MHO và MKO, ta có:
∠(MHO) = ∠(MKO)= 90o
∠(MOH) = ∠(MOK)
OM cạnh huyền chung
Suy ra: ΔMHO = ΔMKO (cạnh huyền - góc nhọn)
Suy ra: MH = MK (2 cạnh tương ứng)
Vậy tập hợp các điểm M cách đều OA và OD là tia phân giác Ox của góc AOD.
Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.
Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.
Đúng 0
Bình luận (0)

