Lập các phân số từ số sau :
a) 1 ; 4 ; 16 ; 64; 256
b) 2 ; 3; 5; 6; 10 ; 15
Bài làm : .
....................................................................................
.....................................................................................



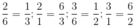
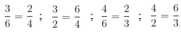
 Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.
Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng. Nếu AB
Nếu AB  đoạn thẳng .(tiết 3- hình 7)
đoạn thẳng .(tiết 3- hình 7)
 sao cho CM = EN.
sao cho CM = EN. Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung
Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung 