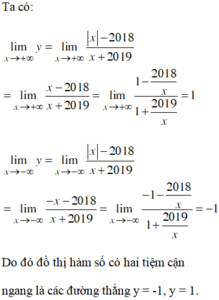(x+y+2z)^2+2018x+2019
NN
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử
a) \(4x^2-12xy+5x^2\)
b) \(\left(x+y+2z\right)^2+\left(x+y-z\right)^2-9z^2\)
c) \(x^4+2019x^2+2018x+2019\)
toán lớp một mà mình lớp 5 ko giải đc :v
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tim x , y thoa man \(y=\sqrt{\frac{2018x+2019}{2017x-2018}}+\sqrt{\frac{2018x+2019}{2018-2017x}}+2018\)
Cho các số x,y thuộc tập n thỏa mãn (x + y - 3)^ 2018 + 2018x (2x - 4)^2020 = 0
Tính giá trị của biểu thức S = (x -1)^2019 +( 2 - y)^2019 = 2018
Nhận xét : ( x + y - 3 )^2018 >=0 và 2018.(2x-4)^2020 >= 0
=> (x+y-3)^2018 + 2018.(2x-4)^2020 >=0
Dấu = xảy ra khi : x + y - 3 = 0 và 2x - 4 = 0 => x = 2 và y = 1
Thay vào bt S :
S = ( 2 - 1)^2019 + (2-1)^2019
= 1^2019 + 1^2019 = 2
Đúng 2
Bình luận (0)
Tính các giá trị biểu thức sau:
a) \(A=x^5-2018x^4+2018x^3-2018x^2+2018x-2019\) biết x=2017
b) \(B=2x^5+5y^3+4\) tại x,y thỏa mãn \(\left(x+1\right)^{20}+\left(y+2\right)^{30}=0\)
a)\(A=x^5-2018x^4+2018x^3-2018x^2+2018x-2019\)
\(A=x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x+1\right)x-2019\)
\(A=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-2019\)
\(A=x-2019=2017-2019=-2\)
b)ta có:\(\left(x+1\right)^{20}+\left(y+2\right)^{30}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Thay vào \(\Rightarrow B=2\cdot\left(-1\right)^5+5\cdot\left(-2\right)^3+4\)
\(B=-2+\left(-40\right)+4=-38\)
Đúng 0
Bình luận (0)
thục hiền đc đó thục hiền ak nay vẫn hoc24 bình thường à ![]()
Đúng 0
Bình luận (0)
Ta có x=2017 => 2018 = x+1 ; 2019= x+2
thay vào ta có : \(A=x^5-\left(x+1\right).x^4+\left(x+1\right).x^3-\left(x+1\right).x^2+\left(x+1\right).x-\left(x+2\right)\) \(=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^x+x-x-2\) \(=\left(x^5-x^5\right)+\left(-x^4+x^4^{ }\right)+\left(x^3-x^3\right)+\left(-x^2+x^2\right)+\left(x-x\right)-2\)=-2
ey học tốt nhá
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Tìm x,y thuộc Z biết: x^3+2018x=2020^2019+4
Số tiệm cận ngang của đồ thị hàm số
y
x
-
2018
x
+
2019
là A. 1. B. 3. C. 2. D. 0.
Đọc tiếp
Số tiệm cận ngang của đồ thị hàm số y = x - 2018 x + 2019 là
A. 1.
B. 3.
C. 2.
D. 0.
Số tiệm cận ngang của đồ thị hàm số y = | x | - 2018 x + 2019 là
A. 1.
B. 3.
C. 2.
D. 0.
Chọn C.
Ta có:
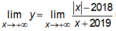
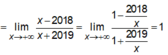
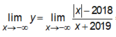
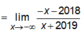
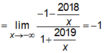
Do đó đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y = -1, y = 1.
Đúng 0
Bình luận (0)
Cho x,y,z là các số thực thỏa mãn : \(\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}\)+z . Tính \(A=2018x+y^{2019}+z^{2019}\)
Tính giá trị của biểu thức: Q(x)= x\(^{32}-2018x^{31}\) + \(2018x^{30}-2018x^{29}\) + ..... + 2018x\(^2-2018x+2019\) tại x = 2017
GIÚP MK VS
MK ĐANG CẦN GẤP!!
tối nay mk phải nộp rùi
giúp mk vs!!
Đúng 0
Bình luận (0)