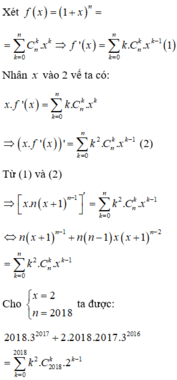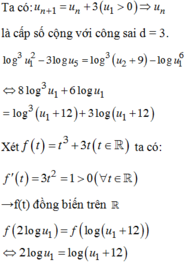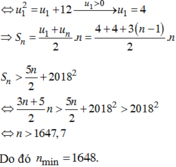cho S=1 + 2018 + 20182 +20183 + 20184 + 20185+ 20186 + 20187
PT
Những câu hỏi liên quan
Tổng
S
1
2
.
C
2018
1
.
2
0
+
2
2
.
C
2018
2
.
2
1
+
3
2
.
C
2018
3
.
2...
Đọc tiếp
Tổng S = 1 2 . C 2018 1 . 2 0 + 2 2 . C 2018 2 . 2 1 + 3 2 . C 2018 3 . 2 2 + . . . + 2018 2 . C 2018 2018 . 2 2017 = 2018 . 3 a . ( 2 b + 1 ) ,
với a, b là các số nguyên dương và (2b+1) không chia hết cho 3.
Tính a+b.
A. 2017
B. 4035
C. 4034
D. 2018
Tổng
S
1
2
.
C
2018
1
.2
0
+
2
2
.
C
2018
2
.2
1
+
3
2
.
C
2018
3
.2
2...
Đọc tiếp
Tổng S = 1 2 . C 2018 1 .2 0 + 2 2 . C 2018 2 .2 1 + 3 2 . C 2018 3 .2 2 + ... + 2018 2 . C 2018 2018 .2 2017 = 2018.3 a . 2. b + 1 với a,b là các số nguyên dương và 2. b + 1 không chia hết cho 3. Tính a + b .
A. 2017
B. 4035
C. 4043
D. 2018
Phân tích số 20187 thành tổng. Cách phân tích nào dưới đây là đúng:
A. 20000 + 100 + 8 + 7
B. 20000 + 100 + 80 + 7
C. 20000 + 1000 + 80 + 7
D. 2000 + 100 + 80 + 7
1+20182
ai nhanh nhất tick
Xem thêm câu trả lời
1) Tìm GTNN của bt :
A=(x-1)(2x-1)(2x2-3x-`)+2018
2) Cho \(x+\dfrac{1}{x}=3\) . Tính gt của bt A= \(x^3+\dfrac{1}{x^3}\)
\(x+\dfrac{1}{x}=3\Leftrightarrow\left(x+\dfrac{1}{x}\right)^3=27\\ \Leftrightarrow x^3+\left(\dfrac{1}{x}\right)^3+3x\cdot\dfrac{1}{x}\left(x+\dfrac{1}{x}\right)=27\\ \Leftrightarrow x^3+\dfrac{1}{x^3}+3\cdot3=27\\ \Leftrightarrow x^3+\dfrac{1}{x^3}=18\)
Đúng 2
Bình luận (0)
khong quy dong hay so sanh E = -7/10^20185+-15/10^2014 và F = -15/10^2013+-7/10^2014
Cho phương trình : mx2 - ( 2m - 1)x + (m-2)=0
1) Giải hệ phương trình vời m=3
2) Tìm m để phương trình đã cho có 2 nghiệm phân biệt x1,x2 thỏa mãn x12 +x22=2018
3) Tìm hệ thức liên hệ giữa các nghiệm ko phụ thuộc vào m
1) Bạn tự giải
2) Ta có: \(\Delta=4m^2-8m+9>0\forall m\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm phân biệt
Theo Vi-ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=m-2\end{matrix}\right.\) (*)
Mặt khác: \(x_1^2+x_2^2=2018\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=2018\)
\(\Rightarrow4m^2-4m+1-2m+4=2018\)
\(\Leftrightarrow4m^2-6m-2013=0\) \(\Leftrightarrow...\)
c) Từ (*) \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2m-1\\2x_1x_2=2m-4\end{matrix}\right.\) \(\Rightarrow x_1+x_2-2x_1x_2=3\)
(Không phụ thuộc vào m)
Đúng 1
Bình luận (0)
A=1x2+2x3+3x4+.....+2017x2018 và B=20183/3. Hãy So sánh A và B
Cần trả lời sớm ạ =]
A = 1.2 + 2.3 + 3.4 + ... + 2017.2018
⇒ 3A = 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + 2017.218.(2019 - 2016)
= 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ... + 2017.2018.2019 - 2016.2017.2018
= 2017.2018.2019
= 2017.2018.2019
B = 2018³/3 ⇒ 3B = 2018³
Ta có:
2017.2019 = (2018 - 1).(2018 + 1)
= 2018² - 1²
= 2018.2018 - 1 < 2018.2018
⇒ 2017.2018.2019 < 2018.2018.2018
⇒ 3A < 3B
⇒ A < B
Đúng 1
Bình luận (0)
Cho dãy u(n) thỏa mãn
log
3
u
1
2
-
3
log
u
5
log
3
u
2
+
9
-
log
u
1
6
và
u
n...
Đọc tiếp
Cho dãy u(n) thỏa mãn log 3 u 1 2 - 3 log u 5 = log 3 u 2 + 9 - log u 1 6 và u n + 1 = u n + 3 u 1 > 0 với mọi n≥1 Đặt S n = u 1 + u 2 + . . . + u n Tìm giá trị nhỏ nhất của n để S n > 5 n 2 + 2018 2
A. 1647
B. 1650
C. 1648
D. 1165
Tính Nhanh:
a)1532-532
b)20202-20192+20182-20172+...+22-12
a) \(153^2-53^2=\left(153-53\right)\left(153+53\right)=100.206=20600\)
b)
\(\left(2020^2-2019^2\right)+\left(2018^2-2017^2\right)+...+\left(2^2-1^2\right)\\ =\left(2020+2019\right)\left(2020-2019\right)+\left(2018+2017\right)\left(2018-2017\right)+...+\left(2+1\right)\left(2-1\right)\\ =2020+2019+2018+2017+...+2+1\\ =\dfrac{\left(2020+1\right)2020}{2}=2041210\)
Đúng 4
Bình luận (0)
Lời giải:
a. $153^2-53^2=(153-53)(153+53)=100.206=20600$
b.
$2020^2-2019^2+2018^2-2017^2+...+2^2-1^2$
$=(2020^2-2019^2)+(2018^2-2017^2)+...+(2^2-1^2)$
$=(2020-2019)(2020+2019)+(2018-2017)(2018+2017)+...+(2-1)(2+1)$
$=2020+2019+2018+2017+...+2+1$
$=\frac{2020.2021}{2}=2041210$
Đúng 2
Bình luận (0)
a) 1532-532=(153-53)(153+53)=100.206=20600
Đúng 0
Bình luận (0)