Tìm nghiệm nguyên của pt
\(xy+3x-5y-8=0\)
a)Tìm nghiệm nguyên của các pt sau: 3x+5y=11 ;9x+7y=51
b)Tìm nghiệm nguyên duơng của pt: xy^2+x+2xy=243y
GIÚP MIK VỚI MAI MÌNH CẦN RỒI
AI LÀM ĐÚNG MIK TICK CHO
Tìm nghiệm nguyên của pt sau:
\(x^2-xy=6x-5y-8\)
PLEASE !!!!
\(x^2-6x+8=x\left(x-1\right)-5\left(x-1\right)+3=\left(x-1\right)\left(x-5\right)+3\)
\(pt\Leftrightarrow y\left(x-5\right)=x^2-6x+8\)
\(x=5\text{ thì pt trở thành }0y=3\text{ (vô nghiệm)}\)
Xét \(x\ne5\)
\(pt\Leftrightarrow y=\frac{x^2-6x+8}{x-5}=x-1+\frac{3}{x-5}\)
Tới đây, bài toán đã đơn giản hơn.
Mình đã lm đến bc đấy r, sau thấy bí quá nên mk ms đăng bài vì mk kb tách \(x-1+\frac{3}{x-5}\)
Tìm nghiệm nguyên x,y của pt: \(x^2-xy=6x-5y-8\)
tìm nghiệm nguyên của pt: 3x^2 + 5y^2 =345
Nhận xét: 345 và 5y^2 chia hết cho 5 nên 3x^2 chia hết cho 5 => x^2 chia hết cho 5 mà 3x^2 < 345 => x^2 < 345 : 3 = 115
=> x^2 = 25; 100 => y2 = 54 hoặc 9
=> chọn x^2 = 100 và y^2 = 9
=> x = 10 ; -10
y = 3; -3
tìm nghiệm nguyên của pt : \(x^3-xy-3x+2y+1=0\)
a) Tìm nghiệm nguyên của PT: xy - 4x = 35 - 5y
b) Tìm nghiệm nguyên của PT: x2 + x + 6 = y2
a,xy-4x=35-5y<=>xy-4x+5y=35<=>xy-4x+5y-20=35-20<=>x(y-4)+5(y-4)=15<=>(x+5)(y-4)=15=1.15=15.1=......
b,x2+x+6=y2<=>4(x2+x+6)=4y2<=>4x2+4x+1+5=4y2<=>(2x+1)2+5=(2y)2<=>(2y)2-(2x+1)2=5<=>(2y-2x-1)(2y+2x+1)=5=1.5=....
Lớp 8 không làm kiểu vậy
a) \(x\left(y-4\right)=35-5y\) với y= 4 không phải nghiệm
\(x=\frac{35-5y}{y-4}=\frac{15-5\left(y-4\right)}{y-4}=\frac{15}{y-4}-5\)
y-4=U(15)={-15,-5,-3,-1,1,3,5,15}
=> y={-11,-1,1,3,5,7,9,19}
=> x={-6,-8,-10,-20,10,0,-2,-4}
b)
\(\left(2x+1\right)^2=4y^2-24+1=4y^2-23\)
Hiệu 2 số chính phương =23 chỉ có thể là 11 và 12
\(\hept{\begin{cases}\left(2y\right)^2=12^2\Rightarrow y=+-6\\\left(2x+1\right)^2=11^2\Rightarrow x=5hoac-6\end{cases}}\)
Tìm nghiệm nguyên của phương trình sau
a,x^2 -xy =6x-5y-8
b, 3x^2 -4y^2=13
a)
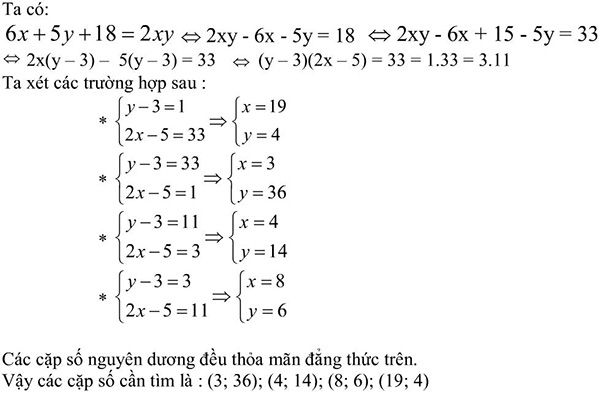
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm
Tìm nghiệm nguyên của phương trình :
a.x^2-xy=6x-5y-8
b.2x^2+3x^2-2y^2=7
Tìm nghiệm nguyên dương của pt : xy+3x-3y=21
xy+3x-3y=21
<=>x(y+3)-3(y+3)-12=0
<=>(x-3)(y+3)=12
đến đây là pt ước số rồi,tự giải
xy + 3x - 3y = 21
=> x.(y + 3) - 3.(y + 3) - 12 =0
=> (y + 3)(x - 3) = 12
Mà x;y \(\in\)Z
=> y+3 ; x-3 \(\in\)Ư(12) = {\(\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\)}
Lại có y > 0
=> y + 3 > 3
=> y + 3 \(\in\left\{4;6;12\right\}\)
Ta có bảng sau:
| y+3 | 4 | 6 | 12 |
| x-3 | 3 | 2 | 1 |
| y | 1 | 3 | 9 |
| x | 6 | 5 | 4 |
Vậy (x;y) = (6;1)
(5;3)
(4;9)