Nhờ các bạn và mọi người giải giúp mình bài bất đẳng thức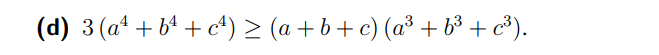
PO
Những câu hỏi liên quan
các bạn ơi giúp mình bài này với:
chứng minh với mọi a,b,c ta có bất đẳng thức:2a2+b2+c2>=2a(b+c)
Cho 60 số tự nhiên liên tiếp,lấy ra ít nhất bao nhiêu số tự nhiên bất kì trong chúng để có tổng hai số tự nhiên liên tiếp:a) chia hết cho 2b)chia hết cho 3 Mình nhờ cậu và các cô,thầy giáo trong ban quản lý giúp với ạ.em đang cần gấp mà hỏi mấy cô chuyên toán cũng không giải được.Mình mong chờ vào các bạn,các thầy cô giáo cả.Nhờ mọi người trình bày bài và có lập luận để đưa ra bài đúng luôn nha1Xin cảm ơn mọi người rất nhiều!
Đọc tiếp
Cho 60 số tự nhiên liên tiếp,lấy ra ít nhất bao nhiêu số tự nhiên bất kì trong chúng để có tổng hai số tự nhiên liên tiếp:
a) chia hết cho 2
b)chia hết cho 3
Mình nhờ cậu và các cô,thầy giáo trong ban quản lý giúp với ạ.em đang cần gấp mà hỏi mấy cô chuyên toán cũng không giải được.Mình mong chờ vào các bạn,các thầy cô giáo cả.Nhờ mọi người trình bày bài và có lập luận để đưa ra bài đúng luôn nha1Xin cảm ơn mọi người rất nhiều!
Nhờ mọi người giải giúp mình bài 4

Nhờ mọi người giải giúp mình bài toán này với:
Tính giá trị biểu thức:
2/5-1/7+3/5x1/3
\(\frac{2}{5}-\frac{1}{7}+\frac{3}{5}.\frac{1}{3}=\frac{14}{35}-\frac{5}{35}+\frac{7}{35}=\frac{16}{35}\)
Đúng 0
Bình luận (0)
\(\frac{2}{5}-\frac{1}{7}+\frac{3}{5}\times\frac{1}{3}\)
\(=\frac{2}{5}-\frac{1}{7}+\frac{1}{5}\)
\(=\frac{9}{35}+\frac{1}{5}\)
\(=\frac{16}{35}\)
Đúng 0
Bình luận (0)
Tìm các số a,b,c thỏa mãn các bất đẳng thức: lal<lb-cl,lbl<la-cl,lcl<la-bl
Các bạn giải giúp mình nhé
1, Chứng minh bất đẳng thức:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}\ge3\forall a\ge1\)
2, Giải phương trình:
\(x\left(x^2-3x+3\right)+\sqrt{x+3}=3\)
Mong mọi người giúp mình với ạ!! Mình cảm ơn nhiều!!
Bài 1:
Vì $a\geq 1$ nên:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}=a+\sqrt{(a-1)^2+4}+\sqrt{a-1}\)
\(\geq 1+\sqrt{4}+0=3\)
Ta có đpcm
Dấu "=" xảy ra khi $a=1$
Đúng 3
Bình luận (0)
Bài 2:
ĐKXĐ: x\geq -3$
Xét hàm:
\(f(x)=x(x^2-3x+3)+\sqrt{x+3}-3\)
\(f'(x)=3x^2-6x+3+\frac{1}{2\sqrt{x+3}}=3(x-1)^2+\frac{1}{2\sqrt{x+3}}>0, \forall x\geq -3\)
Do đó $f(x)$ đồng biến trên TXĐ
\(\Rightarrow f(x)=0\) có nghiệm duy nhất
Dễ thấy pt có nghiệm $x=1$ nên đây chính là nghiệm duy nhất.
Đúng 3
Bình luận (0)
các bạn có thể lấy giúp mình mỗi bất đẳng thức lấy mình 4 bài chứng minh bất đẳng thức có sử dụng các bất đẳng thức sau đay
\(x^3\)+ \(^{y^3}\)\(\ge\)\(xy(x+y)\)
\(\frac{a^3+b^3}{2}\)\(\ge\)\((\frac{a+b}{2})^3\)
Cho x,y>0 thỏa mãn x3+y3=x−y. Chứng minh: x2+y2<1.
Cho x,y>0x,y>0 thỏa mãn x3+y3=x−y. Chứng minh: x2+y2<1.
.............................
Đúng 0
Bình luận (0)
Bài 5: Cho hình chữ nhật ABCD; E, G lần lượt là trung điểm của AD và BC. a. So sánh diện tích hai tứ giác ABGE, EGCD. b. M, N lần lượt là điểm bất kì nằm trên AD và CD. Tìm tỉ số giữa MI và NI Nhờ mọi người giải thích dễ hiểu giúp mình ạ! Cảm ơn rất nhiều ạ!
Đọc tiếp
Bài 5: Cho hình chữ nhật ABCD; E, G lần lượt là trung điểm của AD và BC.
a. So sánh diện tích hai tứ giác ABGE, EGCD.
b. M, N lần lượt là điểm bất kì nằm trên AD và CD. Tìm tỉ số giữa MI và NI
Nhờ mọi người giải thích dễ hiểu giúp mình ạ! Cảm ơn rất nhiều ạ!
a, S 2 tứ giác ABGE, EGCD = nhau
b, thì c ko thông đc chiếc MI và NI, e nhắn lại nhé
Đúng 0
Bình luận (0)

