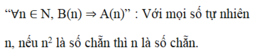Cho n là số tự nhiên chẵn ; n > 4 .CM : n4-4n3-4n2+16n chia hết 384
NH
Những câu hỏi liên quan
Hãy xác đinh bài toán sau: Tìm số các số chẵn trong dãy n số tự nhiên cho trước?A. INPUT: các số chẵn trong dãy n số. OUTPUT: dãy n số tự nhiên .B. INPUT: dãy n số tự nhiên. OUTPUT: số các số chẵn trong dãy n số.C. INPUT: dãy n số tự nhiên . OUTPUT: các số chẵn trong dãy n.D. INPUT: số các số chẵn trong dãy n số. OUTPUT: dãy n số tự nhiên.
Đọc tiếp
Hãy xác đinh bài toán sau: "Tìm số các số chẵn trong dãy n số tự nhiên cho trước"?
A. INPUT: các số chẵn trong dãy n số. OUTPUT: dãy n số tự nhiên .
B. INPUT: dãy n số tự nhiên. OUTPUT: số các số chẵn trong dãy n số.
C. INPUT: dãy n số tự nhiên . OUTPUT: các số chẵn trong dãy n.
D. INPUT: số các số chẵn trong dãy n số. OUTPUT: dãy n số tự nhiên.
Cho số tự nhiên n. Chứng minh rằng: nếu \(n^2\)là số chẵn thì n cũng là số chẵn
Giả sử n là số lẻ
Khi đó: n2 là số lẻ, trái với giả thiết
Vậy n là số chẵn.
Ta có n2 = n.n
mà n2 chẵn
=> n.n chẵn
=> n.n \(⋮\)2
=> có ít nhất 1 số chia hết cho 2
mà n = n => n \(⋮\)2 => n chẵn (đpcm)
Ta có : n^2 = n.n
Mà n^2 là chẵn .
=> n.n chẵn
=> n.n chia hết cho 2
Có ít nhất là 1 chữ số chia hết cho 2
Mà n = n => n chia hết chia hết cho 2
=> n chẵn ( đpcm )
Cho n là số tự nhiên bất kỳ . CMR (n+5).(n+2) là số chẵn
Ta có n là số tự nhiên bất kì có 2 trường hợp:
TH1: n là số lẻ => n+5 là số chẵn( vì lẻ + lẻ = chẵn) => (n+5)(n+2) là số chẵn
TH2: n là số chẵn => n+2 là số chẵn( vì chẵn + chẵn = chẵn) => (n+5)(n+2) là số chẵn
=> Với mọi n thì (n+5)(n+2) là số chẵn
Đúng 0
Bình luận (0)
Cho số tự nhiên n. Xét hai mệnh đề chứa biến :A(n):n là số chẵn, B(n):B(n):
n
2
là số chẵn. Hãy phát biểu mệnh đề “
∀
n
∈
N, B(n) A(n)”. A. Với mọi số tự nhiên n, nếu n là số chẵn thì
n
2
là số chẵn. B. Tồn tại số tự nhiên n, nếu
n
2
là số chẵn thì n là số chẵn. C. Với mọi số tự nhiên n, n...
Đọc tiếp
Cho số tự nhiên n. Xét hai mệnh đề chứa biến :A(n):"n là số chẵn", B(n):B(n):" n 2 là số chẵn". Hãy phát biểu mệnh đề “ ∀ n ∈ N, B(n) => A(n)”.
A. Với mọi số tự nhiên n, nếu n là số chẵn thì n 2 là số chẵn.
B. Tồn tại số tự nhiên n, nếu n 2 là số chẵn thì n là số chẵn.
C. Với mọi số tự nhiên n, nếu n 2 là số chẵn thì n2 là số chẵn.
D. Với mọi số tự nhiên n, nếu n 2 là số chẵn thì n là số chẵn.
1) Chứng minh rằng tổng n số tự nhiên liên tiếp chia hết cho n nếu n là số lẻ ?
2) Chứng minh tổng n số tự nhiên liên tiếp không chia hết cho n nếu n là số chẵn ?
Bài 1 :
Nếu n lẻ thì n + 1 chẵn do đó tổng n số tự nhiên liên tiếp là \(\frac{n.\left(n+1\right)}{2}\) là số chẵn nên không chia hết cho n vì n là số lẻ
Bài 2 :
Nếu n chẵn thì n + 1 lẻ do đó tổng n số tự nhiên liên tiếp là \(\frac{n.\left(n+1\right)}{2}\) là số chẵn nên chia hết cho n vì n là số chẵn
Đúng 0
Bình luận (0)
chứng tỏ rằng:
(a) Tổng của n số tự nhiên liên tiếp là 1 số chia hết cho n nếu n là số lẻ?
(b) Tổng của n số tự nhiên liên tiếp là 1 số chia hết cho n nếu n là số chẵn?
Ta có AEED =dt(AEN)dt(DEN) =hA→MNhD→MN =dt(AMN)dt(DMN)
Mà dt(AMN) = 1/4 dt(ABN) = 1/4 . 1/2 dt(ABC) = 1/8 dt(ABC)
dt(DMN) = dt(ABC) - dt(AMN) - dt(BDM) - dt(CDN) = dt(ABC) - 1/8 dt(ABC) - 3/8 dt(ABC) - 1/4 dt(ABC) = 1/4 dt(ABC)
Vậy AEED =dt(AMN)dt(DMN) =18 dt(ABC)14 dt(ABC) =12 , suy ra AE/AD = 1/3
Cách 2: Giải theo phương pháp bậc THCS (của bạn Lê Quang Vinh)
DN là đường trung bình của tam giác ABC => DN // AB và DN = 1/2 AB
DN // AB => Hai tam giác EAM và EDN đồng dạng => EA/ED = AM/DN = 1/2 (vì AM = 1/4 AB, DN = 1/2 AB)
=> AE/AD = 1/3
k mình nha
Đúng 0
Bình luận (0)
không nên:
Chỉ ghi đáp số mà không có lời giải, hoặc nội dung không liên quan đến câu hỏi.
Đúng 1
Bình luận (0)
cho A là tập hợp các số tự nhiên nhỏ hơn 10, B là tập hợp các số chẵn N* là tập hợp các số tự nhiên khác 0.
A = {0;1;2;3;4;5;6;7;8;9}
B = {0;2;4;6;8;........}
N*={1;2;3;4;5;6;........}
A\(\subset\)N
B\(\subset\)N
N*\(\subset\)N
**** mk nhá!
Đúng 0
Bình luận (0)
A ={0;1;2;3;4;5;.....;10}
B ={0:2;4;6;....}
N* ={1;2;3;4;5;....}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ rằng trong hai số tự nhiên chẵn liên tiếp thì luôn có một và chỉ một số chia hết cho 4(xét hai số tự nhiên chẵn liên tiếp a=2k và a+2=2k+2 ( với k thuộc n) rồi xét trường hợp k là số chẵn k là số lẻ)
CHO A LÀ TẬP HỢP CÁC SỐ TỰ NHIÊN NHỎ HƠN 10 .B LÀ TẬP HỢP VAVS SỐ CHẴN . N HOA LÀ TẬP HỢP CÁC SỐ TỰ NHIÊN KHÁC 0
Chứng tỏ rằng:
(a) Tổng của n số tự nhiên liên tiếp là 1 số chia hết cho n nếu n là số lẻ?
(b) Tổng của n số tự nhiên liên tiếp là 1 số chia hết cho n nếu n là số chẵn?