cho 3 số 1;2;3
a.với 3 số 1;2;3 có thể viết bao nhiêu số thập phân có 2 chữ số ở phần thập phân
b.tính tổng các số vừa tìm được(bằng cách thuận tiện nhất)
Người ta cho vào 1 số vào một cái máy như sau : cho vào số 1 ra số 3 cho số 2 ra số ba cho số 3 ra số 2 cho số 1 ra số 4 cho số 0 ra số 5 cho số 4 ra số 3 . tìm quy luật của nó
không có năm chữ. bốn có ba chữ...
Một số có tổng các chữ số chia cho 9 ( cho 3 ) dư m thì số đó chia cho 9 ( cho 3) cũng dư m
Ví dụ : Số 1543 có tổng các chữ số bằng : 1 + 5 +4 +3 = 13 . Số 13 chia cho 9 dư 4 , chia cho 3 dư 1 . Do đó số 1543 chia cho 9 dư 4 , cho cho 3 dư 1
Một số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m.
Ví dụ: Số 1543 có tổng các chữ số bằng 1 + 5 + 4 + 3 = 13. Số 13 chia 9 dư 4 chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9, cho 3: 1546; 1527; 2468; 1011.
+) 1546 có 1 + 5 + 4 + 6 =16. 16 chia 3 dư 1, chia 9 dư 7.
Do đó 1546 chia 3 dư 1, chia 9 dư 7.
+) 1527 có 1 + 5 + 2 + 7 = 15. Ta thấy 15 chia 9 thư 6 và 15 chia 3 dư 0 nên 1527 chia 9 dư 6, chia hết cho 3.
+) 2468 có 2 + 4 + 6 + 8 = 20. 20 chia 9 dư 2, chia 3 dư 2.
Do đó 2468 chia 3, chia 9 đều dư 2.
+) 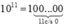 có tổng các chữ số bằng 1. 1 chia 3 và 9 đều dư 1.
có tổng các chữ số bằng 1. 1 chia 3 và 9 đều dư 1.
Do đó 1011 chia 3, chia 9 đều dư 1.
Bài 1: Cho P là số nguyên tố, P > 3 . Hỏi P^2 + 2018 là số nguyên tố hay hợp số?
Bài 2: Cho n là số tự nhiên lớn hơn 3 sao cho n ko chia hết cho 3. CMR n^2 - 1 và n^2 + 1 ko đồng thời là số nguyên tố.
Bài 3: Cho P là số nguyên tố, P > 3 sao cho 8P^2 - 1 là số nguyên tố. CMR 8P^2 + 1 là hợp số.
Bài 4: Cho P là số nguyên tố, P > 3 sao cho P + 2 là số nguyên tố. CMR P + 1 chia hết cho 6.
Vì P>3 nên p có dạng: 3k+1;3k+2 (k E N sao)
=> p^2 :3(dư 1)
=> p^2+2018 chia hết cho 3 và>3
nên là hợp số
2, Vì n ko chia hết cho 3 và>3
nên n^2 chia 3 dư 1
=> n^2-1 chia hết cho 3 và >3 là hợp số nên ko đồng thời là số nguyên tố
3, Ta có:
P>3
p là số nguyên tố=>8p^2 không chia hết cho 3
mà 8p^2-1 là số nguyên tố nên ko chia hết cho 3
Ta dễ nhận thấy rằng: 8p^2-1;8p^2;8p^2+1 là 3 số tự nhiên liên tiếp nên có 1 số chia hết cho 3
mà 2 số trước ko chia hết cho 3
nên 8p^2+1 chia hết cho 3 và >3 nên là hợp số (ĐPCM)
4, Vì p>3 nên p lẻ
=> p+1 chẵn chia hết cho 2 và>2
p+2 là số nguyên tố nên p có dạng: 3k+2 (k E N sao)
=> p+1=3k+3 chia hết cho 3 và>3
từ các điều trên
=> p chia hết cho 2.3=6 (ĐPCM)
Một số có tổng các chữ số chia hết cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m.
VD : Số 1543 có tổng các chữ số bằng : 1 + 5 + 4 + 3 = 13. Số 13 chia cho 9 dư 4, chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9, cho 3 : 1546; 1527; 2468; 1011
Một số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m.
Ví dụ: Số 1543 có tổng các chữ số bằng 1 + 5 + 4 + 3 = 13. Số 13 chia 9 dư 4 chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9, cho 3: 1546; 1527; 2468; 1011
- Số 1546 có tổng 1 + 5 + 4 + 6 = 16. Tổng này chia cho 9 dư 7, chia cho 3 dư 1.
Do đó, số 1546 chia cho 9 dư 7, chia cho 3 dư 1.
- Số 1527 có tổng 1 + 5 + 2 + 7 = 15. Tổng này chia cho 9 dư 6, và chia hết cho 3.
Do đó, số 1527 chia cho 9 dư 6, và chia hết cho 3.
- Số 2468 có tổng 2 + 4 + 6 + 8 = 20. Tổng này chia cho 9 dư 2, chia cho 3 dư 2.
Do đó, số 2468 chia cho 9 dư 2, chia cho 3 dư 2.
- Số 1011 có tổng 1 + 0 + ... + 0 = 1. Tổng này chia cho 9 dư 1, chia cho 3 dư 1.
Do đó, số 1011 chia cho 9 dư 1, chia cho 3 dư 1.
Số 1546 = 1 + 5 + 4 + 6 = 16 : 9 dư 7 và chia 3 dư 1.
Vậy 1546 chia cho 9 dư 7 và chia cho 3 dư 1
Số 1527 = 1 + 5 + 2 + 7 = 15 : 9 dư 6 và chia hết cho 3.
Vậy 1527 chia hết cho 3 và chia 9 dư 6
Số 2468 = 2 + 4 + 6 + 8 = 20 : 9 dư 2 và chia 3 dư 2
Vậy 2468 đều dư 2 khi chia cho 3 và 9.
Số 10^11 có dạng là 100……000 và tổng này luôn luôn chia cho 3 và 9 đều dư 1
Vậy 10^11 chia cho 3 và 9 đều dư 1
- Số 1546 có tổng 1 + 5 + 4 + 6 = 16. Tổng này chia cho 9 dư 7, chia cho 3 dư 1.
Do đó, số 1546 chia cho 9 dư 7, chia cho 3 dư 1.
- Số 1527 có tổng 1 + 5 + 2 + 7 = 15. Tổng này chia cho 9 dư 6, và chia hết cho 3.
Do đó, số 1527 chia cho 9 dư 6, và chia hết cho 3.
- Số 2468 có tổng 2 + 4 + 6 + 8 = 20. Tổng này chia cho 9 dư 2, chia cho 3 dư 2.
Do đó, số 2468 chia cho 9 dư 2, chia cho 3 dư 2.
- Số 1011 có tổng 1 + 0 + ... + 0 = 1. Tổng này chia cho 9 dư 1, chia cho 3 dư 1.
Do đó, số 1011 chia cho 9 dư 1, chia cho 3 dư 1.
Một số có tổng các chữ số chia hết cho 9 (cho 3)dư m dư m thì số đó chia hết cho (3) cũng dư m
Ví dụ Số 1543 có tổng các chữ số bằng :1+5+4+3=13.Số 13 chia cho 9 dư 4,chia cho 3 dư 1 .Do đó số 1543 chia cho 9 dư 4,chia hết cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9 ,cho 3:154;1527:248;1011.
Một số có tổng các chữ số chia hết cho 9 ( cho 3 ) dư m thì số đó chia cho 9 ( cho 3 ) cũng dư m
vis dụ : số 1543 có tổng các chữ số bằng : 1+5+4+3=13. Số 13 chia cho 9 dư 4 chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1
tìm số dư khi chia mỗi số sau cho 9 và 3 : 1546;1527;2468;1011
1546chia cho 9 dư 6 chia cho 3 dư 3
1527 chia cho 9 dư 6 chia cho 3 dư 0
2468 chia cho 9 dư 2 chia cho 3 dư 6
1011thì bí rồi hihi
Chỉ cần tìm số dư trong phép chia có tổng các chữ số chia cho 9 và 3
Vì 1+5+4+6=16 chia cho 9 dư 7 và chia cho 3 dư 1 nên 1546 chia cho 9 dư 7 chia cho 3 dư 1
Vì 1+5+2+7=15 chia cho 9 dư 6 và chia hết cho 3 nên 1527 chia cho 9 dư 6 và chia cho 3 dư 0
Tương tự 2468 chia cho 9 dư 2 và chia cho 3 dư 1
10^11 chia cho 9 dư 1 và chia cho 3 dư 1
Chỉ cần tìm dư trong phép chia tổng các chữ số cho 9, cho 3.
Vì 1 + 5 + 4 + 6 = 16 chia cho 9 dư 7 và chia cho 3 dư 1 nên 1546 chia cho 9 dư 7, chia cho 3 dư 1;
Vì 1 + 5 + 2 + 7 = 15 chia cho 9 dư 6, chia hết cho 3 nên 1526 chia cho 9 dư 6 chia cho 3 dư 0;
Tương tự, 2468 chia cho 9 dư 2, chia cho 3 dư 1;
1011 chia cho 9 dư 1, chia cho 3 dư 1.
1. Dạng tổng quát của số chia hết cho 2 là 2k , dạng tổng quát của số chia cho 2 dư 1 là 2k +1 với k thuộc N.Hãy viết dạng tổng quát số chia hết cho 3, số chia cho 3 dư 1 , số chia cho 3 dư 2.
CHia hết chó 3 là: 3k
Chia 3 dư 1 là; 3k + 1
CHia 3 dư 2 là: 3k + 2
Dạng tổng quát :
Chia hết cho 3 là 3k
Chia cho 3 dư 1 là 3k + 1
Chia cho 3 dư 2 là 3k + 2
Chứng minh rằng:
a.Trong 3 số tự nhiên liên tiếp luôn có 1 số chia hết cho 3.
b.Trong 3 số chẵn liên tiếp luôn có 1 số chia hết cho 3.
c.Trong 3 số lẻ liên tiếp luôn có 1 số chia hết cho 3.