Gieo 8 đồng xu cân đối, tính xác suất để có ít nhất 4 mặt ngửa.
HL
Những câu hỏi liên quan
Gieo 3 đồng xu độc lập , biết xác suất gieo ít nhất 1 mặt ngửa là 7/8 . Tính xác suất để xuất hiện 3 mặt ngửa
Lời giải:
Xác suất để xu 1 ngửa: $\frac{1}{2}$
Xác suất để xu 2 ngửa: $\frac{1}{2}$
Xác suất để xu 3 ngửa: $\frac{1}{2}$
Xác suất để 3 mặt cùng ngửa: $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}$
Đúng 0
Bình luận (0)
Gieo 4 đồng xu cân đối và đồng chất. Xác định biến cố đối của mỗi biến cố sau và tính xác suất của nó
a) “Xuất hiện ít nhất ba mặt sấp”
b) “Xuất hiện ít nhất một mặt ngửa”
Tổng số kết quả có thể xảy ra của phép thử là \(n\left( \Omega \right) = {2^4}\)
a) Biến cố đối của biến cố “Xuất hiện ít nhất ba mặt sấp” là biến cố “ Xuất hiện nhiều nhất một mặt sấp”
Biến cố xảy ra khi trên mặt đồng xu chỉ xuất hiện một hoặc không có mặt sấp nào. Số kết quả thuận lợi cho biến cố là \(C_4^1 + 1 = 5\)
Xác suất của biến cố là \(P = \frac{5}{{{2^4}}} = \frac{5}{{16}}\)
b) Biến cố đối của biến cố “Xuất hiện ít nhất một mặt ngửa” là biến cố “ Không xuất hiện mặt ngửa nào”
Biến cố xảy ra khi tất cả các mặt đồng là mặt sấp. Chỉ có 1 kết quả thuận lợi cho biến cố
Xác suất của biến cố là \(P = \frac{1}{{{2^4}}} = \frac{1}{{16}}\)
Đúng 1
Bình luận (0)
gieo 2 đồng xu A và B một cách độc lập . đồng xu A chế tạo cân đối , đồng xu B chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa . tính xác suất để :
a) khi gieo 2 đồng xu 1 lần thì cả 2 đồng xu đều ngửa .
b) khi gieo 2 đồng xu 2 lần thì 2 lần cả 2 đồng xu đều ngửa .
xác suất mặt ngửa của đồng A là 1/2,của đồng B là 1/4
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
Đúng 0
Bình luận (0)
Gieo 3 đồng xu cân đối đồng chất một cách độc lập. Tính xác suất của biến cố sau:
a) A: cả 3 đồng xu đều ngửa.
b) B: 1 đồng xu sấp 2 đồng xu ngửa.
c) C: có ít nhất 2 đồng xu ngửa .
d) D: có không quá 2 đồng xu sấp.
a: n(A)=1
n(omega)=216
=>P(A)=1/216
b: \(B=\left\{\left(SNN\right);\left(NSN\right);\left(NNS\right)\right\}\)
=>n(B)=3
=>P(B)=3/216=1/72
c: \(C=\left\{\left(NNS\right);\left(NNN\right);\left(SNN\right);\left(NSN\right)\right\}\)
=>P(B)=4/216=1/54
d: \(D=\left\{\left(SSN\right);\left(SNN\right);\left(NSN\right);\left(NNS\right);\left(NSS\right);\left(SNS\right)\right\}\)
=>P(D)=6/216=1/36
Đúng 1
Bình luận (0)
gieo đồng xu 4 lần liên tiếp.tính xác suất có ít nhất 2 lần liên tiếp xuất hiện mặt ngửa
Lời giải:
Mỗi lần gieo sẽ có 2 khả năng (sấp, ngửa). Gieo 4 lần sẽ có thể có $2^4=16$ khả năng xảy ra (không gian mẫu)
Các khả năng tung mà có ít nhất 2 lần xuất hiện mặt ngửa:
NNSS, NNSN, NNNN, NNNS, SNNN, SNNS, SSNN, NSNN
=> có 8 khả năng.
Xác suất: $\frac{8}{16}=\frac{1}{2}$
Đúng 0
Bình luận (0)
Gieo một đồng xu cân đối liên tiếp bốn lần.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.
a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
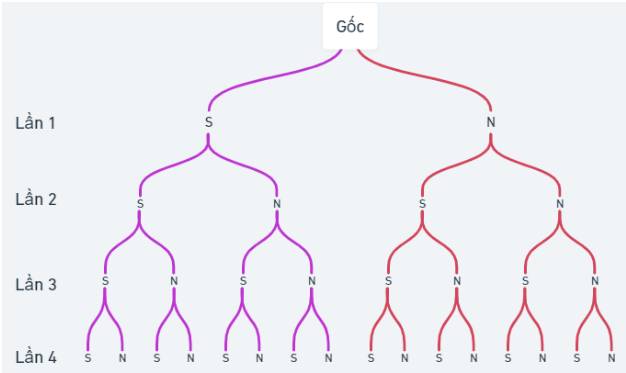
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).
Đúng 0
Bình luận (0)
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn 1 100 .
A. 7
B. 8
C. 9
D. 6
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn 1 100 .
A. 7
B. 8
C. 9
D. 6
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đo 1 2 n < 1 100 ⇔ n < log 1 2 1 100 ⇒ n ≥ 7 .
Ta cần gieo ít nhất 7 lần
Đúng 0
Bình luận (0)
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn
1
100
. A. 7 B. 8 C. 9 D. 6
Đọc tiếp
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn 1 100 .
A. 7
B. 8
C. 9
D. 6
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đó
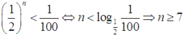
Ta cần gieo ít nhất 7 lần.
Đúng 0
Bình luận (0)
Mỗi lượt ta gieo một con xúc sắc (loại 6 mặt, cân đối), và một đồng xu (cân đối). Tính xác xuất để trong 3 lượt gieo như vậy, có ít nhất một lượt gieo được kết quả con xúc sắc xuất hiện mặt 1 chấm, đồng thời đồng xu xuất hiện mặt sấp A. B. C. D.
Đọc tiếp
Mỗi lượt ta gieo một con xúc sắc (loại 6 mặt, cân đối), và một đồng xu (cân đối). Tính xác xuất để trong 3 lượt gieo như vậy, có ít nhất một lượt gieo được kết quả con xúc sắc xuất hiện mặt 1 chấm, đồng thời đồng xu xuất hiện mặt sấp
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A.
Xác suất một lần gieo được mặt một chấm là ![]() Xác suất để cả ba lần không gieo được mặt một chấm là
Xác suất để cả ba lần không gieo được mặt một chấm là 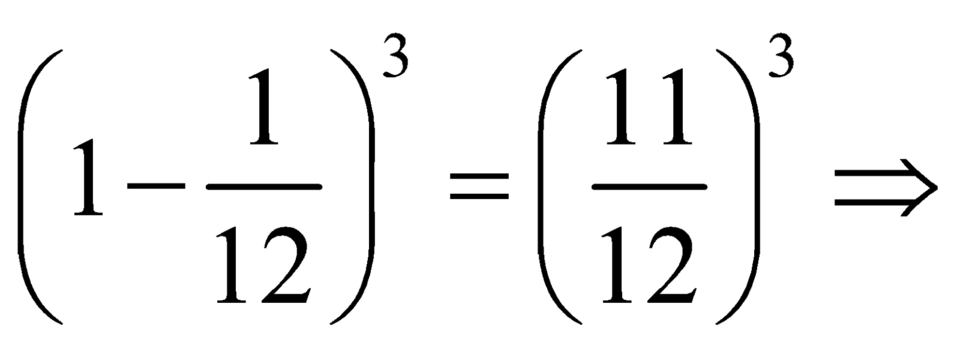 Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là:
Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là: 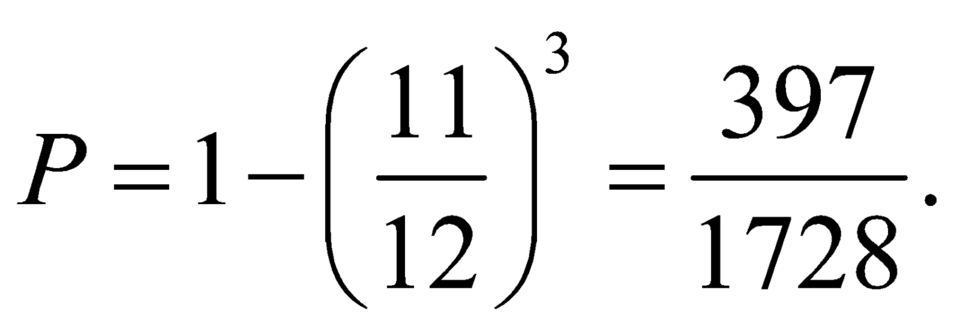
Đúng 0
Bình luận (0)




