Anh chị em CTV giúp em
Cho tam giác ABC có cạnh AB là đường kính cố định của (O;R), đỉnh C di chuyển trên đường tròn đó. AM, BN là các đường trung tuyến.
a) Chứng minh: AM^2+BN^2 không đổi
b) Tìm tập hợp trọng tâm G của tam giác ABC
TL
Những câu hỏi liên quan
Cho tam giác ABC có cạnh AB là đường kính cố định của (O;R), đỉnh C di chuyển trên đường tròn đó. AM, BN là các đường trung tuyến. a) Chứng minh: AM^2+BN^2 không đổi
b) Tìm tập hợp trọng tâm G của tam giác ABC
mấy anh chị giúp em với , em cần gấp :
Cho tam giác ABC trên cạnh AB lấy điểm M sao cho Am bằng 2 lần MB , TRÊN CẠNH AC lấy điểm N sao cho AN= NC . so sánh diện tích tam giác AMN Và tứ giác MNBC
ai giải xong sớm em sẽ ticks cho , cố gắng giúp e nhé
Cho tam giác đều ABC, đường cao AH. Cho M là điểm bất kì trên BC ( M khác B, C ), I là trung điểm của AM. Từ M kẻ ME vuông góc với AB, kẻ MF vuông góc với AC.a) HEIF là hình j? vì sao?b) Gọi G là trọng tâm của tam giác ABC. Chứng minh: EF, MG, HI đồng quy.c) Tìm M trên cạnh BC để EF đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó khi tam giác ABC có cạnh là a.Đây là đề em mới thi hok sinh giỏi mong các anh, chị CTV giúp đỡ! ( có khi mk nhớ nhầm đề đó)
Đọc tiếp
Cho tam giác đều ABC, đường cao AH. Cho M là điểm bất kì trên BC ( M khác B, C ), I là trung điểm của AM. Từ M kẻ ME vuông góc với AB, kẻ MF vuông góc với AC.
a) HEIF là hình j? vì sao?
b) Gọi G là trọng tâm của tam giác ABC. Chứng minh: EF, MG, HI đồng quy.
c) Tìm M trên cạnh BC để EF đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó khi tam giác ABC có cạnh là a.
Đây là đề em mới thi hok sinh giỏi mong các anh, chị CTV giúp đỡ! ( có khi mk nhớ nhầm đề đó)
Hình bạn tự vẽ nha
a) \(\Delta AEM\)vuông tại E có EI là trung tuyến
=> EI = IA (1) => \(\Delta EIA\)cân tại I, có EIM là góc ngoài
=> \(\widehat{EIM}=2\widehat{EAI}\)
Tương tự ta có \(\widehat{HIM}=2\widehat{HAI}\)và IH = IA (2)
Từ (1) và (2) suy ra IE = IH hay \(\Delta EIH\)cân tại I
có \(\widehat{EIH}=\widehat{EIM}+\widehat{HIM}=2\widehat{EAI}+2\widehat{HAI}=2\widehat{EAH}=2\left(90^o-\widehat{ABH}\right)=2\left(90^o-60^o\right)=60^o\)
Vậy EIH là tam giác đều, suy ra EI = EH = IH
Tương tự ta có IHF là tam giác đều, suy ra IH = HF = IF
=> EI = EH = IF = HF
Vậy HEIF là hình thoi
b) \(\Delta ABC\)là tam giac đều nên AH là đường cao cũng là đường trung tuyến
có G là trọng tâm nên \(AG=\frac{2}{3}AH\)(3)
Gọi K là trung điểm AG, suy ra \(AK=KG=\frac{1}{2}AG\)(4)
Từ (3) và (4) suy ra AK = KG = GH
Gọi O là giao điểm của EF và IH, suy ra OI = OH
\(\Delta AMG\)có IK là đường trung bình nên IK // MG
\(\Delta IKH\)có OG là đường trung bình nên IK // OG
=> M, O, G thẳng hàng (tiên đề Ơ-clit)
Vậy EF, MG, HI đồng quy
c) HEIF là hình thoi nên \(EF\perp HI\)
\(\Delta EIH\)đều có EO là đường cao nên \(EO=EI\sqrt{\frac{3}{4}}\)(bạn tự chứng minh)
\(EF=2EO=2EI\sqrt{\frac{3}{4}}=AM\sqrt{\frac{3}{4}}\)(5)
EF đạt GTNN khi AM đạt GTNN
mà \(AM\ge AH\)nên EF đạt GTNN khi M trùng H
Khi đó AM là đường cao trong tam giác đều ABC nên ta cũng có \(AM=AB\sqrt{\frac{3}{4}}=a\sqrt{\frac{3}{4}}\)(6)
Từ (5) và (6) suy ra \(EF=a\left(\sqrt{\frac{3}{4}}\right)^2=\frac{3}{4}a\)
Vậy EF đạt GTNN là \(\frac{3}{4}a\)khi M là chân đường cao hạ từ A xuống BC.
Đúng 0
Bình luận (0)
Ở đề không có điểm K, sao ở câu hỏi lại có điểm K vậy em?
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Vho tam giác ABC vuông tại A đường cao AH Có AB= 12cm ; AH = 9cm Giúp em với anh chị em cảm ơn anh chị nhiều 🥺
Áp dụng PTG vào ΔABH ta có: \(AH^2+BH^2=AB^2\Rightarrow BH=\sqrt{12^2-9^2}=3\sqrt{7}\)
Áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow BC=\dfrac{12^2}{3\sqrt{7}}=\dfrac{48\sqrt{7}}{7}\)
Áp dụng PTG vào ΔABC có: \(AB^2+AC^2=BC^2\Rightarrow AC=\sqrt{\left(\dfrac{48\sqrt{7}}{7}\right)^2-12^2}=\dfrac{36\sqrt{7}}{7}\)
Đúng 0
Bình luận (0)
Anh chị nào giỏi hình giup em với ạ
Cho tam giác ABC vuông A,AB=6cm,AC=8cm.Tìm tâm bán kính của đường tròn ngoại tiếp tam giác ABC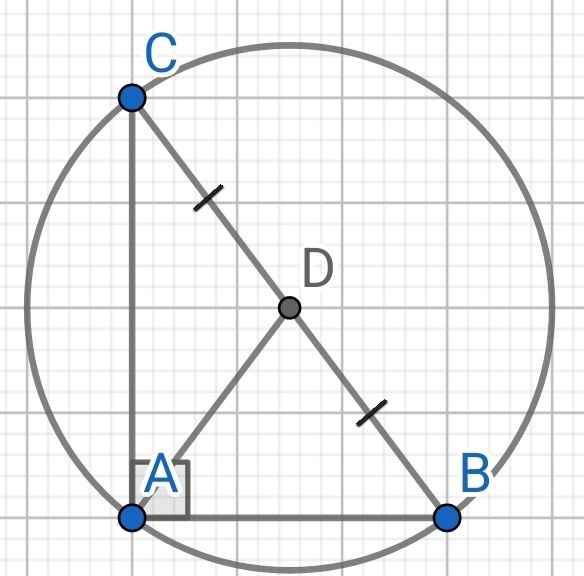
∆ABC vuông tại A (gt)
BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
BC = 10 (cm)
Gọi D là trung điểm của BC
AD là đường trung tuyến ứng với cạnh huyền BC
AD = BD = CD = BC : 2 = 5 (cm)
Ba điểm A, B, C cùng nằm trên đường tròn tâm D, bán kính AD = 5 cm
Đúng 2
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn tâm O có AD là đường kính .tiếp tuyến tại D cắt BC tại P .PO cắt AB,AC tại M và N. chứng minh OM=ON
(CÁC ANH CHỊ GIẢI CHO EM THEO CÁCH LỚP 9 ĐƯỢC KO)
tick nhaCho đường tròn tâm O,đường AB cố định.H là điểm cố định thuộc đoạn OA (H ko trùng O và A).Qua H vẽ đường thẳng vuông góc với AB cắt đường tròn O tại C và D.Gọi K là điểm tùy ý thuộc cung lớn CD(K ko trùng các điểm C,D và B).I là giao điểm của AK và CDChứng Minh : khi K thay đổi trên cung lớn CD của đường tròn tâm O thì tâm đường tròn ngoại tiếp tam giác KCI luôn thuộc 1 đường thẳng cố định MONG ANH CHỊ GIÚP ĐỠ (EM ĐANG CẦN GẤP)
Đọc tiếp
Cho đường tròn tâm O,đường AB cố định.H là điểm cố định thuộc đoạn OA (H ko trùng O và A).Qua H vẽ đường thẳng vuông góc với AB cắt đường tròn O tại C và D.Gọi K là điểm tùy ý thuộc cung lớn CD(K ko trùng các điểm C,D và B).I là giao điểm của AK và CD
Chứng Minh : khi K thay đổi trên cung lớn CD của đường tròn tâm O thì tâm đường tròn ngoại tiếp tam giác KCI luôn thuộc 1 đường thẳng cố định
MONG ANH CHỊ GIÚP ĐỠ (EM ĐANG CẦN GẤP)
cho tam giác abc vuông tại a có ad là đường phân giác . tính bd biết ab=6cm,ac=8, bc=10cm
anh chị ơi giúp em nhé em đang cần gấp nha
cho tam giác ABC vuông tại A có BC=2a; B = 300 và đường tròn (O) đường kính AB (như hình vẽ). Quay hình tròn (O) và tam giác ABC quanh cạnh AB cố định thì được một hình cầu và một hình nón. so sánh diện tích mặt cầu và diện tích toàn phần của hình nón