Tìm n\(\in\)\(ℕ\)biết:
n2 + n + 1 \(⋮\)n + 2; n > 0
HN
Những câu hỏi liên quan
TL
3 tháng 6 2021 lúc 15:12
Tìm n thuộc N biết:
n2 + n + 4 chia hết cho n + 1
n2 + n + 4 = n(n + 1) + 4 chia hết cho n + 1
Suy ra :
4 chia hết cho n + 1
Vậy : n + 1 ∈ Ư(4) = {-1;1;-2;2;-4;4}
Với n + 1 = - 1 <=> n = -2
Với n + 1 = 1 <=> n = 0
Với n + 1 = -2 <=> n = -3
Với n + 1 = 2 <=> n = 1
Với n + 1 = -4 <=> n = -5
Với n + 1 = 4 <=> n = 3
Đúng 3
Bình luận (1)
Giải:
\(n^2+n+4⋮n+1\)
\(\Rightarrow n.\left(n+1\right)+4⋮n+1\)
\(\Rightarrow4⋮n+1\)
\(\Rightarrow n+1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Vì \(n\in N\) nên \(n+1\in\left\{1;2;4\right\}\)
Ta có bảng giá trị:
| n+1 | 1 | 2 | 4 |
| n | 0 | 1 | 3 |
Vậy \(n\in\left\{0;1;3\right\}\)
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
1.Tìm số nguyên x,biết:
a) 2/x-1/+/1-x/=9
2.tìm các cặp số x,y thỏa mãn:
(2x+1)(5-y)=6
3.tìm số nguyên "n" ,biết:
n2+3n-5 chia hết cho n+3
4.tìm tát cả các số nguyên x thỏa mãn:
(x2-1)(x2-6)<0
GIÚP MIK VỚI,ĐÚNG CHO 5 LIKE!!
HH
13 tháng 2 2023 lúc 21:58
Tìm n ∈ \(ℕ\), n ≥ 1 sao cho tổng 1! + 2! + 3! + ... + n! là 1 số chính phương
Xét các trường hợp:
\(n=1\Leftrightarrow1!=1=1^2\) là số chính phương
\(n=2\Leftrightarrow1!+2!=3\) không phải là số chính phương
\(n=3\Leftrightarrow1!+2!+3!=9=3^3\) là số chính phương
\(n\ge4\Leftrightarrow1!+2!+3!+4!=33\) còn \(5!,6!,7!,...,n!\) đều có tận cùng là \(0\Rightarrow1!+2!+3!+...+n!\) có tận cùng là chữ số 3 nên không phải là số chính phương
Vậy \(n\in\left\{1;3\right\}\).
Đúng 2
Bình luận (0)
Tìm x \(\in\)\(ℕ\)để:
(2.n + 1) \(⋮\)( 3 - n)
CẦN GẤP!!!!
Dùng phương pháp quy nạp chứng minh rằng :
\(n^n\ge\left(n+1\right)^{n-1}\forall n\in\)ℕ∗
Cho
I
n
∫
0
1
e
-
n
x
1
+
e
-
x
d
x
n
∈
ℕ
Đặt
u...
Đọc tiếp
Cho I n = ∫ 0 1 e - n x 1 + e - x d x n ∈ ℕ Đặt u n = ( I 1 + I 2 ) + 2 ( I 2 + I 3 ) + . . . . . + n ( I n + I n + 1 ) . Biết lim u n = L Mệnh đề nào sau đây là đúng?
Tìm n ∈ ℕ đ ể 3 n + 4 ⋮ n + 1
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Tách. Bước 2. Áp dụng tính chất chia hết của một tổng. Bước 3. Tìm n+1. Bước 4. Tìm n. |
Ta có: 3 n + 4 = 3 n + 3 + 1 = 3 n + 1 + 1 Để 3 n + 4 ⋮ n + 1 thì 1 ⋮ n + 1 ⇒ n + 1 = 1 ⇒ n = 0 |
Đúng 0
Bình luận (0)
Cho dãy số
u
n
thỏa mãn
u
1
1
u
n
3
u
n
-...
Đọc tiếp
Cho dãy số u n thỏa mãn u 1 = 1 u n = 3 u n - 1 + 1 ∀ n ∈ ℕ , n ≥ 2 . Tìm giá trị nhỏ nhất của n để log 9 u n > 100
A. 102
B. 101
C. 202
D. 201
Chọn đáp án D
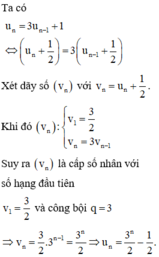
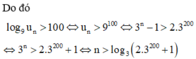
Vậy số tự nhiên n nhỏ nhất thỏa mãn điều kiện trên là n 0 = 201
Đúng 0
Bình luận (0)
Với n\(\in\)\(ℕ^∗\),ta định nghĩa n!=1x2x3x...x n.Hỏi tổng S= 1!+2!+...+2023! có chia hết cho 5 hay ko?Vì sao?
không nhé, vì từ 5! trở đi sẽ chia hết cho 5 (vì 1x2x3x4x5x.... (chia hết cho 5))
Đặt phần từ 5! -> 2023! = b (b chia hết cho 5)
ta còn: 1!+2!+3!+4!+b
=1+1x2+1x2x3 + 1x2x3x4 + b
=1+2+6+24+b
=33+b
mà 33 không chia hết cho 5 trong khi b chia hết cho 5
=> S không chia hết cho 5
Đúng 0
Bình luận (0)