[(7-2)4 - 252 ] . 20182019 + 150 : 5 . 2
các anh chị giúp e với ạ!
Cho đa thức:
Q=23x^3y^3+17x^3y^3-50x^3y^3+(-2xy)^3
Tính giá trị của Q tại |x-1|=1 và y=-1/2
các anh chị giúp e với
\(Q=23x^3y^3+17x^3y^3-50x^3y^3+(-2xy)^3\)
\(Q=23x^3y^3+17x^3y^3-50x^3y^3+(-8)x^3y^3\)
\(Q=(23+17-50-8)x^3y^3\)
\(Q=-18x^3y^3\)
---
\(|x-1|=1\)
\(TH1:\) \(x-1=1\)
⇒ \(x=1+1=2\)
\(TH2: x-1=-1\)
⇒ \(x=(-1)+1=0\)
---
Tính giá trị của \(Q\) tại \(|x-1|=1\) và \(y=\dfrac{-1}{2}\)
\(TH1: x=2; y=\dfrac{-1}{2}\)
\(Q=-18.2^3.(\dfrac{-1}{2})^3\)
\(Q=-18.8.(\dfrac{-1}{8})^3\)
\(Q=36\)
\(TH1: x=0; y=\dfrac{-1}{2}\)
\(Q=-18.0^3.(\dfrac{-1}{2})^3\)
\(Q=0\)
Vậy \(Q\) ∈ {\({36;0}\)}
Ta có: \(Q=23x^2y^3+17x^3y^3-50x^3y^3+\left(-2xy\right)^3\)
\(=-10x^3y^3-8x^3y^3\)
\(=-18x^3y^3\)
Ta có: |x-1|=1
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Thay x=2 và y=-1/2 vào Q, ta được:
\(Q=-18\cdot2^3\cdot\left(-\dfrac{1}{2}\right)^3=-18\cdot8\cdot\dfrac{-1}{8}=18\)
Thay x=0 và y=-1/2 vào Q, ta được:
\(Q=-18\cdot0^3\cdot\left(-\dfrac{1}{2}\right)^3=0\)
Nhầm, \(Q\) ∈ {\(18;0\)} mới đúng ạ ;-;
ANH CHỊ GIÚP EM TIẾNG ANH 7 CÂU 1 VÀ 2 VỚI Ạ .CHIỀU E THI Ạ.EM CẢM ƠN ANH CHỊ RẤT NHIỀU Ạ!!!
Question 2: David has volunteered for 2 years
Question 3: I think collecting stamps is interesting
ANH CHỊ GIÚP EM TIẾNG ANH 7 CÂU 1 VÀ 2 VỚI Ạ .CHIỀU E THI Ạ.EM CẢM ƠN ANH CHỊ RẤT NHIỀU Ạ!!!

mình làm câu 2, 3 rồi nhé
https://hoc24.vn/cau-hoi/anh-chi-giup-em-tieng-anh-7-cau-1-va-2-voi-a-chieu-e-thi-aem-cam-on-anh-chi-rat-nhieu-a.3054793966970
câu 1: Lan had a high fever, so she stayed home from school yesterday
Một phép chia có tổng số chia và số bị chia và số dư là 150. Tìm số bị chia và số chia biết phép chia có thương là 5 , số dư là 6
Anh chị ơi bài này e ko hiểu anh chị giúp e với . cám ơn anh chị ạ !
Giải:
Tổng của số chia và số bị chia là:
\(150-6=144\)
Vì số bị chia chia cho số chia sẽ có thương là 5 nên số bị chia sẽ gấp số chia 5 lần .
Số bị chia là : \(144\div\left(5+1\right)\times5=120\)
Số chia là: \(144-120=24\)
Anh chị ơi giúp em bài kiểm tra lớp 9 với ạ .em còn câu 5 6 7 anh chị giúp em với .Em cảm ơn rất nhiều ạ!!!!!!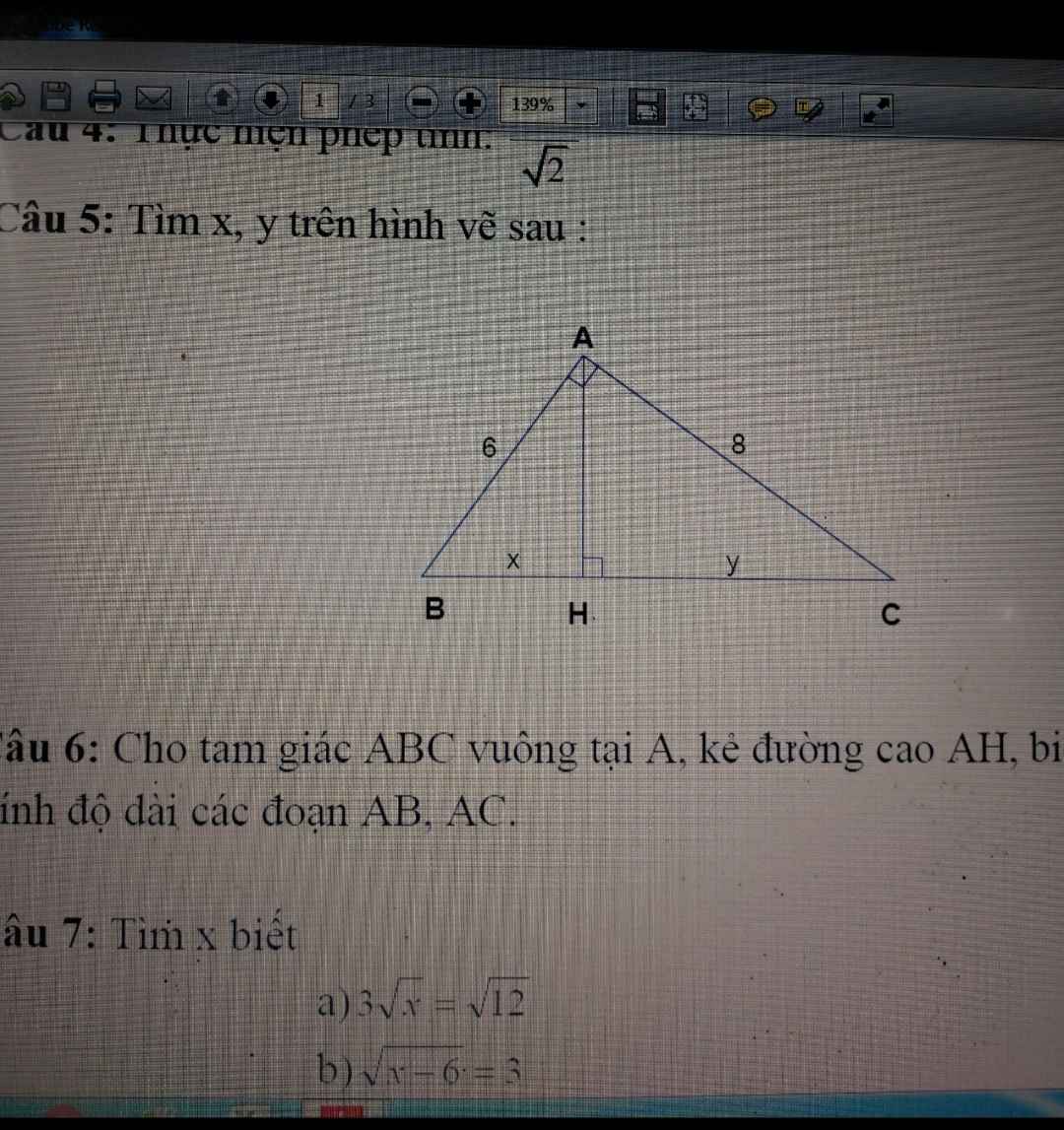
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
Câu 5:
Áp dụng định lý Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{6^2+8^2}\\ \Rightarrow BC=10\)
Áp dụng HTL ta có: \(x.BC=AB^2\Rightarrow x.10=6^2\Rightarrow x=3,6\)
Áp dụng HTL ta có: \(x.BC=AC^2\Rightarrow x.10=8^2\Rightarrow x=6,4\)
câu 5:
x=3,6
y=6,4
câu 6:
không biết
câu 7:
a)ĐKXĐ:
b) ĐKXĐ:
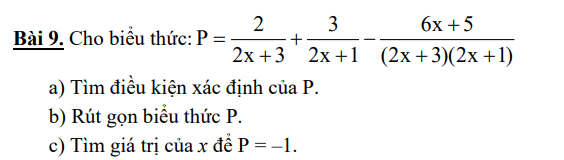
ANh chị ơi giúp e với ạ! e đg cần gấp! cảm ơn anh chị nhiều ạ<3
a) ĐKXĐ: \(\left\{{}\begin{matrix}2x+3\ne0\\2x+1\ne0\\\left(2x+3\right)\left(2x+1\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{3}{2}\\x\ne-\dfrac{1}{2}\\\left(2x+3\right)\left(2x+1\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{3}{2}\\x\ne-\dfrac{1}{2}\end{matrix}\right.\)
b) \(\Rightarrow P=\dfrac{2\left(2x+1\right)+3\left(2x+3\right)-6x-5}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{4x+2+6x+9-6x-5}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{4x+6}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{2\left(2x+3\right)}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{2}{2x+1}\)
c) \(P=-1\Rightarrow\dfrac{2}{2x+1}=-1\\ \Rightarrow2=-2x-1\\ \Rightarrow2x=-3\\ \Rightarrow x=-\dfrac{3}{2}\)
Anh chị ơi giúp e làm bài này với ạ, e cần gấp ý ạ:(( E cảm ơn các anh chị nhiều ạ<3

Bài 6
\(a,ĐK:x\ne\pm5\\ b,P=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\\ c,P=-3\Leftrightarrow\dfrac{1}{x+5}=-3\Leftrightarrow-3\left(x+5\right)=1\Leftrightarrow x=-\dfrac{16}{3}\\ \Leftrightarrow Q=\left(3x-7\right)^2=\left[3\cdot\left(-\dfrac{16}{3}\right)-7\right]^2=529\)
Bài 7:
\(a,ĐK:x\ne\pm3\\ b,P=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\\ b,P=4\Leftrightarrow4\left(x-3\right)=4\Leftrightarrow x=4\)
Điều kiện (x≠5, x≠-5)
\(P=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2x+10}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}+\dfrac{2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}-\dfrac{2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{x-5+2\left(x+5\right)-2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}=\dfrac{1}{x+5}\)
Anh chị giúp e câu 3 và câu 4 với ạ. E cảm ơn

giúp e với anh chị ơi! Đừng chép mạng nhé ạ! E cảm ơn anh chị rất rất nhiều ạ