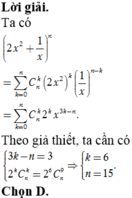Trong khai triển (x3+2x2+x+2)n thành đa thức, hệ số của x3n-3 là 18683n/3. Tìm n
TU
Những câu hỏi liên quan
Với n là số nguyên dương, gọi
a
3
n
-
3
là hệ số của
x
3
n
-
3
trong khai triển thành đa thức của
x
2
+
1
n...
Đọc tiếp
Với n là số nguyên dương, gọi a 3 n - 3 là hệ số của x 3 n - 3 trong khai triển thành đa thức của x 2 + 1 n x + 2 n . Tìm n để a 3 n - 3 = 26 n
A: 5
B: 6
C: 7
D: 8
Ta có : 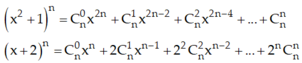
Dễ dàng kiểm tra n=1; n=2 không thoả mãn điều kiện bài toán.
Với n ≥ 3 thì dựa vào khai triển ta chỉ có thể phân tích
![]()
Do đó hệ số của x3n-3 trong khai triển thành đa thức của
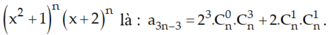
Suy ra  hoặc n = 5
hoặc n = 5
Vậy n=5 là giá trị cần tìm.
Chọn A.
Đúng 0
Bình luận (0)
Với n là số nguyên dương, gọi
a
3
n
−
3
là hệ số của
x
3
n
−
3
trong khai triển thành đa thức của
x
2
+
1
n...
Đọc tiếp
Với n là số nguyên dương, gọi a 3 n − 3 là hệ số của x 3 n − 3 trong khai triển thành đa thức của x 2 + 1 n x + 2 n . Tìm n để a 3 n − 3 = 26 n .
A. n = 7
B. n = 5
C. n = 6
D. n = 4
Biết rằng hệ số của
x
3
trong khai triển nhị thức Newton
2
x
2
+
1
x
n
(với
x
≠
0
) bằng
2
6
C
n
9
. Tìm n. A....
Đọc tiếp
Biết rằng hệ số của x 3 trong khai triển nhị thức Newton 2 x 2 + 1 x n (với x ≠ 0 ) bằng 2 6 C n 9 . Tìm n.
A. n =12
B. n =13
C. n =14
D. n =15
Tìm hệ số của
x
3
trong khai triển f(x)
(
2
x
+
1
)
25
thành đa thức? A.300. B.2300. C.1200. D.18400.
Đọc tiếp
Tìm hệ số của x 3 trong khai triển f(x)= ( 2 x + 1 ) 25 thành đa thức?
A.300.
B.2300.
C.1200.
D.18400.
Tìm hệ số của
x
3
trong khai triển
x
x
0
⇔
f
x
0
0
f...
Đọc tiếp
Tìm hệ số của x 3 trong khai triển x = x 0 ⇔ f ' x 0 = 0 f ' ' x 0 > 0 thành đa thức?
A. 300
B.2300
C. 1200
D.18400
Tìm hệ số của số hạng chứa
x
15
trong khai triển
(
2
x
3
-
3
)
n
thành đa thức, biết n là số nguyên dương thỏa mãn hệ thức
A
n
3
+
C
n
1
8
C
n
2
+
49...
Đọc tiếp
Tìm hệ số của số hạng chứa x 15 trong khai triển ( 2 x 3 - 3 ) n thành đa thức, biết n là số nguyên dương thỏa mãn hệ thức A n 3 + C n 1 = 8 C n 2 + 49
A. 6048
B. 6480
C. 6408
D. 4608
Tìm hệ số của \(x^4\) trong khai triển của biểu thức P = \(\left(1-x-3x^3\right)^n\) thành đa thức, biết n là số nguyên dương thoả mãn \(2\left(C^2_2+C^2_3+...+C^2_n\right)=3A^2_{n+1}\).
\(C_2^2+C_3^2+...+C_n^2=C_3^3+C_3^2+C_4^2+...+C_n^2\) (do \(C_2^2=C_3^3=1\))
\(=C_4^3+C_4^2+C_5^2+...+C_n^2=C_5^3+C_5^2+...+C_n^2\)
\(=...=C_n^3+C_n^2=C_{n+1}^3\)
Do đó:
\(2C_{n+1}^3=3A_{n+1}^2\Leftrightarrow\dfrac{2.\left(n+1\right)!}{3!.\left(n-2\right)!}=\dfrac{3.\left(n+1\right)!}{\left(n-1\right)!}\)
\(\Leftrightarrow n-1=9\Rightarrow n=10\)
\(\Rightarrow P=\left(1-x-3x^3\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(-x-3x^3\right)^k\)
\(=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^k\left(x+3x^3\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^kx^i.3^{k-i}.x^{3\left(k-i\right)}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^k.3^{k-i}.x^{3k-2i}\)
Ta có: \(\left\{{}\begin{matrix}0\le i\le k\le10\\i;k\in N\\3k-2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;2\right);\left(4;4\right)\)
Hệ số: \(C_{10}^2C_2^1\left(-1\right)^2.3^1+C_{10}^4C_4^4.\left(-1\right)^4.3^0=...\)
Đúng 1
Bình luận (1)

\(\Rightarrow he-so:\left[{}\begin{matrix}C^9_{10}C^1_9\left(-3\right)^{10-9}\left(-1\right)=270\\C^{10}_{10}C^4_{10}\left(-3\right)^{10-10}.\left(-1\right)^4=210\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong khai triển
2
x
2
+
1
x
n
∑
k
0
n
C
n
k
.2
n
−
k...
Đọc tiếp
Trong khai triển 2 x 2 + 1 x n = ∑ k = 0 n C n k .2 n − k x 2 n − k . 1 x k , x ≠ 0 hệ số của x 3 là 2 6 C n 9 . Tính n
A. n = 12
B. n = 13
C. n = 14
D. n = 15
Đáp án D
Ta có 2 x 2 + 1 x n = ∑ k = 0 n C n k .2 n − k . 1 x k = ∑ k = 0 n C n k . 2 n − k x 2 n − 3 k
Cho 2 n − 3 k = 3 ⇒ C n k .2 n − k = 2 6 . C n 9 .
Giải hệ 2 n − 3 k = 3 C n k .2 n − k = 2 6 . C n 9
Hệ này tương đối khó giải, thử 4 đáp án ta được ⇔ n = 15 k = 9
Đúng 0
Bình luận (0)
Trong khai triển
2
x
2
+
1
x
n
∑
k
0
n
C
n
k
.
2
n
-...
Đọc tiếp
Trong khai triển 2 x 2 + 1 x n = ∑ k = 0 n C n k . 2 n - k x 2 n - k . 1 x k
( x ≠ 0 ) hệ số của x 3 là 2 6 C n 9 . Tính n
A. n = 12
B. n = 13
C. n = 14
D. n = 15