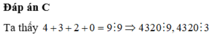CMR:2^1234+3^4321+3 chia hết cho 22
QH
Những câu hỏi liên quan
Trong tập hợp 4319 , 4321 , 4321 , 4322 , số nào chia hết cho cả 3 và 9
A. 4319
B. 4321
C. 4320
D. 4322
Tìm dư khi lấy 43211234 chia 73
1 CMR a, 101234 + 2 chia hết cho 3
b, 10789 + 8 chia hết cho 9
cần gấp nhanh nha
cho a=111..111(2006 chữ số 1) b=111...111(1975 chữ số 1)
cmr: a.b+1234 chia hết cho 3
cho a=111..111(2006 chữ số 1) b=111...111(1975 chữ số 1)
cmr: a.b+1234 chia hết cho 3
cho tổng A=1+2+22+23+...+299
a) Rút gọn A b) CMR: A chia hết cho 3 và 5 |
c) CMR: A không chia hết cho 7
d) Tìm chữ số tận cùng của A
a) \(A=1+2+2^2+2^3+...+2^{99}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{100}\)
\(\Rightarrow A=2A-A=2+2^2+...+2^{100}-1-2-2^2-...-2^{99}=2^{100}-1\)
b) \(A=1+2+2^2+...+2^{99}=\left(1+2+2^2+2^3\right)+2^4\left(1+2+2^2+2^3\right)+...+2^{96}\left(1+2+2^2+2^3\right)\)
\(=15+2^4.15+...+2^{96}.15=15\left(1+2^4+...+2^{96}\right)\)
\(=3.5\left(1+2^4+...2^{96}\right)\) chia hết cho 3 và 5
c) \(A=1+2+2^2+...+2^{99}\)
\(=1+2\left(1+2+2^2\right)+...+2^{97}\left(1+2+2^2\right)\)
\(=1+2.7+...+2^{97}.7=1+7\left(2+...+2^{97}\right)\) chia 7 dư 1
=> A không chia hết cho 7
Đúng 2
Bình luận (0)
Bài 1:Cho a=11....11(104 cơ số 1) ; b= 22..22(17 cơ số 2)
CMR:ab-2 chia hết cho 3
Bài 2: Cho Ạ=16x+14y ; B=27x-41y
CMR nếu Ạ chia hết 11 thì B chia hết 11 và ngược lại
a) 10^1234 + 2 chia hết cho 3
b) 10^789 + 9 chia hết cho 9
a/Ta có:
10^1234 = 100....0000 (1234 số 0)
Vậy 10^1234+2 = 100...0002 (1233 số 0)
Tổng các chữ số của 10^1234 là 1+2 = 3 chia hết cho 3 =>10^1234+2 chia hết cho 3
b/Bài b nếu tính theo cách giống như bài a thì ta có tổng các chữ số là : 10 không chia hết cho 9
Có thể là do đề của bạn sai hoặc có cách chứng minh khác mà mình không biết
Đúng 0
Bình luận (0)
\(\dfrac{8642-1234}{4321X3-\left(4321+1234\right)}X999=\)
\(=\dfrac{7408}{12963-5555}\cdot999=999\)
Đúng 2
Bình luận (0)
\(7408/12963-5555*999=7408/7408*999=1*999=999\)
Đúng 2
Bình luận (0)
\(\dfrac{8642-1234}{4321\times3-\left(4321+1234\right)}\times999=\dfrac{7408}{12963-5555}\times999=\dfrac{7408}{7408}\times999=1\times999=999\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời