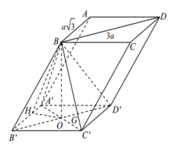
Cho hai hình thoi ABCD và A'B'C'D' có AC=A'C' và BD=B'C'.Cm hai hình thoi đó bằng nhau.vì sao
DS
Những câu hỏi liên quan
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh
a
3
, BD 3a, hình chiếu vuông góc của B lên mặt phẳng (ABCD) là trung điểm của AC. biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDDC) bằng
21
7
. Tính theo a thể tích khối hộp ABCD.ABCD
Đọc tiếp
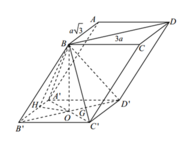
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a 3 , BD = 3a, hình chiếu vuông góc của B lên mặt phẳng (A'B'C'D') là trung điểm của A'C'. biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDD'C') bằng 21 7 . Tính theo a thể tích khối hộp ABCD.A'B'C'D'
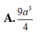
![]()
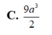
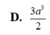
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh
a
3
, BD 3a. hình chiếu vuông góc của B lên mặt phẳng (ABCD) là trung điểm của AC. Biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDDC) bằng
21
7
. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện ABCD. A. a B. 2a C. 3a D.
a
2
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a 3 , BD = 3a. hình chiếu vuông góc của B lên mặt phẳng (A'B'C'D') là trung điểm của A'C'. Biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDD'C') bằng 21 7 . Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A'BC'D'.
A. a
B. 2a
C. 3a
D. a 2
Cho hình lập phương ABCD ABCD có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BD và BC. A.
a
2
B.
a
2
2
C.
a
3
3
D.
a
6
6
Đọc tiếp
Cho hình lập phương ABCD A'B'C'D' có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BD' và B'C.
A. a 2
B. a 2 2
C. a 3 3
D. a 6 6
Đáp án D.
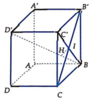
Cách 1: Gọi I là giao điểm của BC' và B'C . Trong B C ' D ' kẻ I H ⊥ B D ' tại H.
Ta có
B C ' ⊥ B ' C D ' C ' ⊥ B ' C B C ' , D ' C ' ∈ B C ' D ' ⇒ B ' C ⊥ B C ' D ' ⇒ B ' C ⊥ I H
Suy ra IH là đường vuông góc chung của BD' và B ' C ⇒ d B D ' , B ' C = I H .
Hai tam giác vuông BC'D' và BHI đồng dạng
⇒ I H D ' C ' = B I B D ' = a 2 2 a 3 = 6 6 ⇒ I H = a 6 6
Ta chọn D.
Cách 2: (Tọa độ hóa . Độc giả tự thực hiện)
Đúng 0
Bình luận (0)
Cho hình thoi \(ABCD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Biết \(AC = 6\)cm; \(BD = 8\)cm. Tính độ dài cạnh của hình thoi \(ABCD\)
Do \(ABCD\) là hình thoi nên hai đường chéo vuông góc với nhau tạo ra 4 góc vuông.
Áp dụng ĐL Pythagore vào 1 trong các tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{6}{2}} \right)}^2} + {{\left( {\frac{8}{2}} \right)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\) (cm)
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB 20 cm, OA 16cm. Diện tích hình thoi ABCD là: A.
384
c
m
2
B.
192
c
m
2
C.
320
c
m
2
D.
240
c
m
2
Đọc tiếp
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 20 cm, OA = 16cm. Diện tích hình thoi ABCD là:
A. 384 c m 2
B. 192 c m 2
C. 320 c m 2
D. 240 c m 2
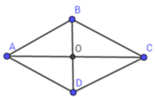
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB 10 cm, OA 6cm. Diện tích hình thoi ABCD là: A.
48
c
m
2
B.
96
c
m
2
C.
24
c
m
2
D.
40
c
m
2
Đọc tiếp
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 10 cm, OA = 6cm. Diện tích hình thoi ABCD là:
A. 48 c m 2
B. 96 c m 2
C. 24 c m 2
D. 40 c m 2
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
C
13
,
A
C
5
. Tính diện tích xung quanh
S
x
q
của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hai hình chữ nhật ABCD và ABCD. A....
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A ' C = 13 , A C = 5 . Tính diện tích xung quanh S x q của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hai hình chữ nhật ABCD và A'B'C'D'.
A. S x q = 120 π
B. S x q = 130 π
C. S x q = 30 π
D. S x q = 60 π
Đáp án D
Chiều cao hình hộp h = A ' C 2 − A C 2 = 12.
Bán kính đáy của hình trụ là: r = A C 2 = 5 2
Khi đó S x q = 2 π r h = 60 π .
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có O là giao điểm hai đường chéo. Biết AB = 58 cm và AC : BD = 1,05. Khi đó AC = ? cm
Vì : \(\frac{AC}{BD}=1,05\)
\(\Rightarrow\frac{\frac{1}{2}AC}{\frac{1}{2}BD}=1,05\)
\(\Rightarrow\frac{AO}{BO}=1,05\)
\(\Rightarrow AO=1,05.BO\)
Xét \(\Delta AOB\) vuông tại O ( vì O là giao điểm 2 đường chéo của hình thoi )
\(AO^2+BO^2=AB^2\) ( định lí Py ta go )
\(\left(1,05.BO\right)^2+BO^2=58^2\)
\(2,1025BO^2=3364\)
\(\Rightarrow BO^2=1600\)
\(\Rightarrow BO=40\) ( vì \(BO>0\) )
\(\Rightarrow AC=\left(BO.1,05\right).1=84\left(cm\right)\)
Vậy ..............
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD ABCD có khoảng cách giữa hai đường thẳng AB và BC bằng khoảng cách giữa hai đường thẳng BC và AB và bằng
2
a
5
5
. Khoảng cách giữa hai đường thẳng AC và BD là
a
3
3
. Tính thể tích V của khối hộp chữ nhật đã cho A.
V
a
3...
Đọc tiếp
Cho hình hộp chữ nhật ABCD A'B'C'D' có khoảng cách giữa hai đường thẳng AB và B'C bằng khoảng cách giữa hai đường thẳng BC và AB' và bằng 2 a 5 5 . Khoảng cách giữa hai đường thẳng AC và BD' là a 3 3 . Tính thể tích V của khối hộp chữ nhật đã cho
A. V = a 3
B. V = 8 a 3
C. V = 2 a 3
D. V = 3 a 3
Đáp án C.
Giả sử các kích thước của hình hộp chữ nhật là A B = x , A D = y , A A ' = z . Trong đó x , y , z > 0 . Để giải bài toán, ta phân tích từng dữ kiện có trong đề bài.
1. Khoảng cách giữa hai đường thẳng AB và B'C bằng 2 a 5 5 .
Ta có
A B / / C D C D ⊂ A ' B ' C D A B ⊄ A ' B ' C D ⇒ A B / / A ' B ' C D ⇒ d A B ; B ' C = d A B ; A ' B ' C D
= d A ; A ' B ' C D = A H = 2 a 5 5 với H là hình chiếu của A trên .
Từ 1 A H 2 = 1 A A ' 2 + 1 A D 2 ⇒ 1 y 2 + 1 z 2 = 5 4 a 2 (1)
2. Khoảng cách giữa hai đường thẳng BC và AB' bằng 2 a 5 5 .
Tương tự, ta chứng minh được
B C / / A B ' C ' D ⇒ d B C ; A B ' = d B C ; A B ' C ' D
= B K = 2 a 5 5
với K là hình chiếu của B trên AB'.
Từ 1 B K 2 = 1 B A 2 + 1 B B ' 2 ⇒ 1 x 2 + 1 z 2 = 5 4 a 2 (2)
3. Khoảng cách giữa hai đường thẳng AC và BD' là a 3 3 .
Gọi O = A C ∩ B D ⇒ O là trung điểm của BD. Gọi I là trung điểm của DD' thì OI là đường trung bình của Δ B D D ' ⇒ O I / / B D ' ⇒ B D ' / / A C I
⇒ d B D ' ; A C = d B D ' ; A C I = d D ' ; A C I = d D ; A C I
Ta thấy DI, DA, DC đôi một vuông góc với nhau nên:
1 d 2 D ; A C I = 1 D A 2 + 1 D C 2 + 1 D I 2 = 1 D A 2 + 1 D C 2 + 4 D D ' ⇒ 1 x 2 + 1 y 2 + 4 z 2 = 3 a 2
(3)
Giải hệ phương trình gồm (1), (2) và (3) ta tìm được: x = y = z , z = 2 a .
Vậy thể tích của khối hộp chữ nhật đã cho là V = x y z = a . a .2 a = 2 a 3 (đvtt).
Đúng 0
Bình luận (0)
Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD
Giúp mình với! Mình cần gấp!
Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (gt)
⇒O là trung điểm của AC và BD
⇒AO=AC2 và DO=BD2
=> AO=6/2=3(cm) và DO = 8/2= 4cm
AC vuông góc BD TẠI O ( vì ABCD là hình thoi )
tam giác ADO vuông góc tại O có AD bình = AO bình + DO bình ( định lý pytago)
=> AD2 =3 bình + 4 bình = 25 => AD= 5cm
Vậy AB=BC=DC=AD=5cm