Cho tam giác ABC vuông tại A.Tìm tập hợp điểm M sao cho MB^2 +MC^2=MA^2
HL
Những câu hỏi liên quan
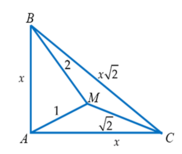
Cho tam giác ABC vuông cân tại A và điểm M nằm trong tam giác sao cho MA1, MB2, MC
2
. Tính góc
A
M
C
⏜
Đọc tiếp
Cho tam giác ABC vuông cân tại A và điểm M nằm trong tam giác sao cho MA=1, MB=2, MC= 2 . Tính góc A M C ⏜
![]()
![]()
Cho tam giác ABC cố định . tìm điểm M hoặc tập hợp điểm M sao cho
véc tơ MA + 3 véc tơ MB - 2 véc tơ MC = véc tơ 0
3 véc tơ MA - véc tơ MB - 2 véc tơ MC = véc tơ 0
Cho tam giác ABC. Tập hợp các điểm M sao cho
M
A
→
+
M
B
→
M
C
→
+
M...
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M sao cho M A → + M B → = M C → + M B → | là:
A. Đường trung trực của BC
B. Đường tròn tâm I, bán kính R = 2AB với I nằm trên cạnh AB sao cho IA = 2IB
C. Đường trung trực của EF với E, F lần lượt là trung điểm của AB và BC
D. Đường tròn tâm I, bán kính R = 2AC với I nằm trên cạnh AB sao cho IA = 2IB
Gọi E và F lần lượt là trung điểm của AB; BC. Khi đó, ta có
M A → + M B → = M C → + M B → ⇔ 2 M E → = 2 M F → ⇔ M E → = M F →
Do đó, M thuộc đường trung trực của EF.
Đáp án C
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại B và tồn tại một điểm M nằm trong tam giác sao cho MA : MB : MC = 1: 2 : 3. Tính AMB
cho tam giác ABC tìm tập hợp điểm M sao cho \(\overrightarrow{MB}^2+\overrightarrow{MC}^2-\overrightarrow{MA}^2=0\)
Cho tam giác ABC. Tìm Tập hợp các điểm M sao cho \(2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+\overrightarrow{2MB}+\overrightarrow{3MC}\right|\)
Gọi G là trọng tâm ΔABC
⇒ VT = 6MG
VP = \(\left|2\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)+\overrightarrow{MC}-\overrightarrow{MA}\right|\)
VP = \(\left|6\overrightarrow{MG}+\overrightarrow{AC}\right|\)
Xác định điểm I sao cho \(6\overrightarrow{IG}+\overrightarrow{AC}=\overrightarrow{0}\) (cái này chắc bạn làm được)
VP = \(\left|6\overrightarrow{MI}+6\overrightarrow{IG}+\overrightarrow{AC}\right|\)
VP = 6 MI
Khi VT = VP thì MG = MI
⇒ M nằm trên đường trung trực của IG
Tập hợp các điểm M : "Đường trung trực của IG"
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại B và tồn tại một điểm M nằm trong tam giác sao cho
MA : MB : MC = 1 : 2 : 3. Tính góc AMB
Cho tam giác ABC đều cạnh a. Tìm tập hợp điểm M thoả: MA^2+MB^2+MC^2= 2a^2
Gọi I là trọng tâm tam giác:
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
Kẻ đường cao AH
\(\Rightarrow AI=\dfrac{2}{3}AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow AI^2=\dfrac{a^2}{3}=BI^2=CI^2\)
\(MA^2+MB^2+MC^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2\) \(\Leftrightarrow2a^2=3MI^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+IA^2+IB^2+IC^2\)
\(\Leftrightarrow2a^2=3MI^2+3IA^2\)
\(\Leftrightarrow2a^2=3MI^2+\dfrac{3.a^2}{3}\)
\(\Leftrightarrow MI^2=\dfrac{a^2}{3}\)
\(\Leftrightarrow MI=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow M\in\) đường tròn tâm I bán kính \(\dfrac{a\sqrt{3}}{3}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC, tập hợp các điểm M sao cho
M
A
→
+
M
B
→
+
M
C
→
6
là: A. một đư...
Đọc tiếp
Cho tam giác ABC, tập hợp các điểm M sao cho M A → + M B → + M C → = 6 là:
A. một đường thẳng đi qua trọng tâm của tam giác.
B. đường tròn có tâm là trọng tâm của tam giác và bán kính bằng 6.
C. đường tròn có tâm là trọng tâm của tam giác và bán kính bằng 2.
D. đường tròn có tâm là trọng tâm của tam giác và bán kính bằng 18