Tìm a và b để đa thức P(x) = x4 + 4x3 + ax2 + bx - 5 chia cho x - 2 dư 9, chia cho x+5 dư -5
YY
Những câu hỏi liên quan
tìm các số nguyên a và b để đa thức A(x)=x^3+ax^2+bx+2 chia chi đa thức B(x)=x+1 còn dư 5 và chia cho C(x)=x+2 dư 8
tìm a,b để đa thức f(x)= x3 + ax2 + bx +3 chia cho g(x)= x+1 dư 5 và chia cho h(x)= x+2 dư 8
b) Tìm m để đa thức
A
(
x
)
x
4
–
x
3
+
6
x
2
–
x
+
m
chia cho đa thức
B
(
x
)
x
2
–
x
+
5
có dư bằng 2
Đọc tiếp
b) Tìm m để đa thức A ( x ) = x 4 – x 3 + 6 x 2 – x + m chia cho đa thức B ( x ) = x 2 – x + 5 có dư bằng 2
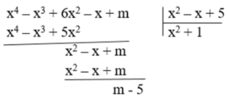
A(x) chia cho B(x) có số dư bằng 2. Vậy m – 5 = 2 ⇒ m = 7.
Đúng 0
Bình luận (0)
Cho H(x)=4x3+ax2+bx+c. biết H(x) chi x-1 dư 4, chia x+2 dư 35, chia x-3 dư 120. Tìm a, b, c
Các pạn giải hộ mk nha . Sáng mai mk phải nộp bài rùi huhu
Đúng 0
Bình luận (0)
Xác định a,b để đa thức A= x3 + ax2 + bx +2 chia cho x +1 thì dư 5 và chia cho x + 2 thì dư 8
Lời giải:
Theo định lý Bê-du về phép chia đa thức:
Số dư của $A(x)$ khi chia cho $x+1$ là:
$A(-1)=(-1)^3+a(-1)^2+b(-1)+2=-1+a-b+2=5$
$\Rightarrow a-b=4(1)$
Số dư của $A(x)$ khi chia cho $x+2$ là:
$A(-2)=(-2)^3+a(-2)^2+b(-2)+2=-8+4a-2b+2=8$
$\RIghtarrow 4a-2b=14$
$\Rightarrow 2a-b=7(2)$
Từ $(1); (2)\Rightarrow a=3; b=-1$
Đúng 0
Bình luận (0)
tìm a b c sao cho đa thức x4 + ax2 + bx + c chia hết cho đa thuc ( x - 3 )3
(Câu trả lời của alibaba nguyễn đúng mà hài!!!)
Sơ đồ Horner hoạt động như sau:
| 1 | 0 | a | b | c | |
| 3 | 1 | 3 | a+9 | 3a+b+27 | 9a+3b+c+27 |
| 3 | 1 | 6 | a+27 | 6a+b+108 | 27a+6b+c+351 |
| 3 | ... | ... | ... | ... | ... |
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) tìm a để đa thức 4x3 - 2x2+ a chia hết cho đa thức 2x - 3
b) Tìm giá trị a để đa thức 3x3 + 2x2 + x + a chia cho đa thức x + 1 có số dư bằng 2
\(a,\Leftrightarrow4x^3-2x^2+a=\left(2x-3\right).a\left(x\right)\)
Thay \(x=\dfrac{3}{2}\Leftrightarrow4.\dfrac{27}{8}-2.\dfrac{9}{4}+a=0\)
\(\Leftrightarrow\dfrac{27}{2}-\dfrac{9}{2}+a=0\\ \Leftrightarrow a=-9\)
\(b,\Leftrightarrow3x^3+2x^2+x+a=\left(x+1\right).b\left(x\right)+2\)
Thay \(x=-1\Leftrightarrow-3+2-1+a=2\Leftrightarrow a=4\)
Đúng 1
Bình luận (1)
Cho đa thức A = 3 10 5 x x a 3 2 và B = 3 1 x
a) Hãy đặt phép chia và tìm dư R trong phép chia A cho B.
b) Tìm a để đa thức A chia hết cho đa thức B
Bài 1: Tìm đa thức bậc 7 nhận \(x=\sqrt[7]{\dfrac{3}{5}}+\sqrt[7]{\dfrac{5}{3}}\) làm nghiệm
Bài 2: Tìm a, b, c để \(ax^2+bx+c⋮x+2\) và chia \(x^2-1\) dư \(x+5\)
Bài 1:
Đặt \(a=\sqrt[7]{\dfrac{3}{5}};b=\sqrt[7]{\dfrac{5}{3}}\Rightarrow\left\{{}\begin{matrix}a+b=x\\ab=1\end{matrix}\right.\)
Ta có \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\)
\(\Rightarrow a^3+b^3=x\left(x^2-3\right)=x^3-3x\)
Ta có \(a^4+b^4=\left(a^2+b^2\right)^2-2\left(ab\right)^2=\left[\left(a+b\right)^2-2ab\right]^2-2\left(ab\right)^2\)
\(\Rightarrow a^4+b^4=\left(x^2-2\right)^2-2=x^4-4x^2+2\)
\(\Rightarrow\left(a^3+b^3\right)\left(a^4+b^4\right)=\left(x^3-3x\right)\left(x^4-4x^2+2\right)\\ =x^7-3x^5-4x^5+12x^3+2x^3-6x\\ =x^7-7x^5+14x^3-6x\)
Lại có \(\left(a^4+b^4\right)\left(a^3+b^3\right)=a^7+b^7+\left(ab\right)^3\left(a+b\right)=\dfrac{3}{5}+\dfrac{5}{3}+x=\dfrac{34}{15}+x\)
\(\Rightarrow x^7-7x^5+14x^3-6x=\dfrac{34}{15}+x\\ \Rightarrow15x^7-105x^5+210x^3-105x-34=0\left(1\right)\)
Vậy (1) nhận \(x=\sqrt[7]{\dfrac{3}{5}}+\sqrt[7]{\dfrac{5}{3}}\) làm nghiệm
Đúng 6
Bình luận (0)
Bài 2 đa thức bậc 2 chia đa thức bậc 2 dư đa thức bậc 1 ??
Đúng 1
Bình luận (1)






