Đặt phép chia:
2x4 - 10x3 - x2 + 15x - 3 ) : (2x2 - 3)
MF
Những câu hỏi liên quan
Làm tính chia: (2x4 + 10x3 + x2 + 15x - 3) : (2x2 + 3)
\(=\left(2x^4+3x^2+10x^3+15x-2x^2-3\right):\left(2x^2+3\right)\\ =\left(2x^2+3\right)\left(x^2+5x-1\right):\left(2x^2+3\right)\\ =x^2+5x-1\)
Đúng 1
Bình luận (0)
2x4 - 10x3 - x2 + 15x - 3 ) : (2x2 - 3)
(2x4 - 10x3 - x2 +15x - 3): (2x2 - 3) = x2 - 5x + 1
Đúng 0
Bình luận (0)
Thực hiện phép chia:a) (
x
3
-
2
x
2
- 15x + 36) : (x + 4);b) (
2
x
4
+
2
x
3
+
3
x
2
- 5x - 20) : (
x
2
+ x + 4);c) (2
x
3...
Đọc tiếp
Thực hiện phép chia:
a) ( x 3 - 2 x 2 - 15x + 36) : (x + 4);
b) ( 2 x 4 + 2 x 3 + 3 x 2 - 5x - 20) : ( x 2 + x + 4);
c) (2 x 3 + 11 x 2 + 18x-3) : (2x + 3);
d) (2x3 + 9x2 +5x + 41) : (2x2 - x + 9).
a) Đa thức thương x 2 – 6x + 9.
b) Đa thức thương 2 x 2 – 5.
c) Đa thức thương x 2 + 4x + 3 và đa thức dư -12.
d) Đa thức x + 5 và đa thức dư x – 4.
Đúng 0
Bình luận (0)
Cho hai đa thức A
2
x
4
-
10
x
3
+
3
x
2
-
3
x
+
2
; B
2
x
2
+
1
.Tìm đa thức dư R trong phép chia A cho B rồi viết A B.Q + R
Đọc tiếp
Cho hai đa thức A= 2 x 4 - 10 x 3 + 3 x 2 - 3 x + 2 ; B = 2 x 2 + 1 .Tìm đa thức dư R trong phép chia A cho B rồi viết A= B.Q + R
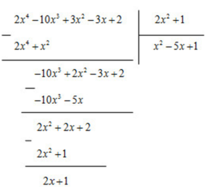
A = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
Vậy đa thức dư R của phép chia A cho B là R = 2x + 1. Khi đó:
2 x 4 - 10 x 3 + 3 x 2 - 3 x + 2 = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
Đúng 0
Bình luận (0)
a) Thực hiện phép chia đa thức (2x4 - 6x3 +12x2 - 14x + 3) cho đa thức (x2 – 4x +1)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
Đúng 3
Bình luận (0)
Kết quả của phép tính ( x2 – 5x)(x + 3 ) là :
A. x3 – 2x2 – 15x
B. x3 + 2x2 + 15x
C. x3 + 2x2 – 15x
D. x3 – 2x2 + 15x
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)
Thực hiện phép chia: (2x4 – 4x3 + 5x2 + 2x – 3):(2x2 - 1)
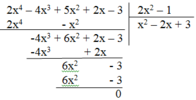
Vậy (2x4 – 4x3 + 5x2 + 2x – 3) : (2x2 – 1) = x2 – 2x + 3.
Đúng 0
Bình luận (0)
Bài 1:
a)Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
b)Tìm a để đa thức x^4-x^3+6x^2-x+a chia hết cho đa thức x^2-x+5
a: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)