Giả sử \(0< a;b;c\le1\). CMR
\(\frac{a\left(b+c\right)}{bc\left(a+1\right)}+\frac{b\left(c+a\right)}{ca\left(b+1\right)}+\frac{c\left(a+b\right)}{ab\left(c+1\right)}\ge\frac{6}{1+\sqrt[3]{abc}}\)
LH
Những câu hỏi liên quan
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: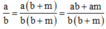 
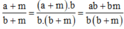
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó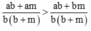 
Hay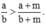 
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
giả sử a,b là nghiệm của phương trình \(x^2+px+1=0\)
giả sử c,d là nghiệm của phương trình \(x^2+qx+1=0\)
chứng minh hệ thức: (a-c)(a+d)(b+d)=\(q^2-p^2\)
PA
25 tháng 6 2021 lúc 0:18
Giả sử: a,b >0 và m,n ∈ Z*
Tìm min của: \(P=ax^m+b\dfrac{1}{x^n}
\) với x>0
Lời giải:
Áp dụng BĐT Cô - si:
\(P=ax^m+\frac{b}{x^n}=\frac{a}{n}x^m+\frac{a}{n}x^m+...+\frac{a}{n}x^m+\frac{b}{mx^n}+...+\frac{b}{mx^n}\)
\(=(m+n)\sqrt[m+n]{(\frac{a}{n})^n.x^{mn}.(\frac{b}{m})^m.\frac{1}{x^{mn}}}\)
\(=(m+n)\sqrt[m+n]{\frac{a^nb^m}{n^n.m^m}}\)
Đúng 0
Bình luận (0)
Cho phân số
a
b
a
,
b
∈
ℕ
,
b
≠
0
Giả sử
a
b
1
và
m
∈
ℕ
,
m
≠
0
. Chứng minh rằng:
a
b
a
+
m
b
+...
Đọc tiếp
Cho phân số a b a , b ∈ ℕ , b ≠ 0
Giả sử a b < 1 và m ∈ ℕ , m ≠ 0 . Chứng minh rằng: a b < a + m b + m
Thực hiện quy đồng: a b = a b + m b b + m = a b + a m b 2 + b m
a + m b + m = b a + m b b + m = a b + b m b 2 + b m
Vì a b < 1 ⇒ a < b ⇒ a b + a m < a b + b m
Từ đó ta thu được a b < a + m b + m
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)Giả sử a/b1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:a/ba+m/b+mgiúp mình với
Đọc tiếp
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a/b<1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a/b<a+m/b+m
giúp mình với
giả sử X=a/m ,Y=b/m (a,b,m "thuộc"Z ,m>0) va x
Gọi M và N là 2 điểm khác phía với đường xy , MN cắt xy tại O. Trên tia Ox lấy A: OA=2
a) Giả sử MAx =1200. Chứng minh Ay phân giác MAN
b) Trên Oy lấy B giả sử MBN=1000; MBO=400. Tính OBN
c) Muốn cho Õ lấy A,B thì OB phải bằng bao nhiêu
LP
3 tháng 6 2023 lúc 18:14
Giúp mình 2 câu này với.
1. Giả sử left(u_nright)_{nge1} là dãy số dương. Nếu limlimits_{ }u_nainleft[0;+inftyright] thì limlimits_{ }sqrt[n]{u_1u_2...u_n}a
2. Giả sử left(u_nright)_{nge1} là dãy số dương. Nếu limlimits_{ }dfrac{u_{n+1}}{u_n}ainleft[0;+inftyright] thì limlimits_{ }sqrt[n]{u_n}a
Đọc tiếp
Giúp mình 2 câu này với.
1. Giả sử \(\left(u_n\right)_{n\ge1}\) là dãy số dương. Nếu \(\lim\limits_{ }u_n=a\in\left[0;+\infty\right]\) thì \(\lim\limits_{ }\sqrt[n]{u_1u_2...u_n}=a\)
2. Giả sử \(\left(u_n\right)_{n\ge1}\) là dãy số dương. Nếu \(\lim\limits_{ }\dfrac{u_{n+1}}{u_n}=a\in\left[0;+\infty\right]\) thì \(\lim\limits_{ }\sqrt[n]{u_n}=a\)
Mình quên không nói là đề bài yêu cầu chứng minh 2 bổ đề trên.
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục và a0. Giả sử với mọi
x
∈
0
;
a
ta có f(x)0 và f(x).f(a-x) 1. Tính
I
∫
0
a
d
x
1
+
f
(
x
)
Đọc tiếp
Cho hàm số f(x) liên tục và a>0. Giả sử với mọi x ∈ 0 ; a ta có f(x)>0 và f(x).f(a-x) = 1. Tính I = ∫ 0 a d x 1 + f ( x )
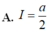
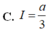
