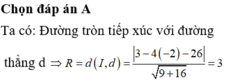Tìm điều kiện của m để đường thẳng 3x−4y+m0 tiếp xúc với đường tròn tâm O, bán kính R1.
Đọc tiếp
Tìm điều kiện của m để đường thẳng 3x−4y+m=0 tiếp xúc với đường tròn tâm O, bán kính R=1.
VN
Những câu hỏi liên quan
Viết phương trình đường tròn Tâm I tiếp xúc với đường thẳng d: 3x-4y-31=0 tại điểm M(1:7) và bán kính R=5
Trên mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx - 1 (m ≠ 0). Tìm m để đường thẳng (d) tiếp xúc với đường tròn có tâm tại gốc tọa độ O và bán kính R = \(\dfrac{1}{\sqrt{10}}\)
Cho đường tròn có tâm và góc tọa độ O bán kính 1 và đường thẳng (d) có phương trình 3x-4y=m^2-m+3
a) Xác định m để đường thẳng tiếp xúc vs đường tròn
b) Khoảng cách từ O đến đường thẳng có giá trị nhỏ nhất là bao nhiêu?
Trong mặt phẳng tọa độ Oxy, tính bán kính đường tròn tâm I(1;-2) và tiếp xúc với đường thẳng d: 3x-4y-26=0
A. R = 3
B. R = 5
C. R = 9.
D. R = 3 5
Cho điểm A(7; 4) và đường thẳng ∆: 3x – 4y + 8 = 0. Bán kính đường tròn tâm A và tiếp xúc với ∆ là:
A.13/5
B.3/5
C.7/5
D.3/2
ĐÁP ÁN A
Bán kính đường tròn tâm A và tiếp xúc với ∆ là
R = d A , ∆ = 3.7 − 4.4 + 8 3 2 + − 4 2 = 13 5
Đúng 0
Bình luận (0)
Bài tập :
B1 Viết phương trình đường tròn (C1) có bán kính R1 = 1 , tiếp xúc với trục Ox và có tâm nằm trên đường thẳng denta : 3x - y +7 = 0
B2 Cho đường tròn (C) : x2 + y2 - 2x - 4y - 4 = 0 và đường thẳng (d) : 3x + 4y +4 = 0 . Chứng minh rằng (d) tiếp xúc với (C)
Cho đường tròn (C) có tâm I(2; 5) và tiếp xúc với đường thẳng ∆: 3x – 4y – 6 0. Khi đó (C) có bán kính là: A.R 2 B.
R
2
2
C. R 3 D.R 4
Đọc tiếp
Cho đường tròn (C) có tâm I(2; 5) và tiếp xúc với đường thẳng ∆: 3x – 4y – 6 = 0. Khi đó (C) có bán kính là:
A.R = 2
B. R = 2 2
C. R = 3
D.R = 4
Đường tròn có bán kính là R = d I , ∆ = 3.2 − 4.5 − 6 3 2 + − 4 2 = 4
ĐÁP ÁN D
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB và 1 điểm C trên AB với ACa, BCb. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn đường kính AB tại P. Dựng đường tròn tâm P bán kính r1, tiếp xúc với CA,CD và tiếp xúc với nửa đường tròn đường kính AB. Dựng đường tròn tâm Q bán kính r2 tiếp xúc với CB,CD và tiếp xúc với nửa đường tròn đường kính AB. Gọi r là bán kính đường tròn nội tiếp tam giác ABDa/ Tính r1,r2 theo a,bb/Tìm đẳng thức liên hệ giữa r,r1,r2
Đọc tiếp
Cho đoạn thẳng AB và 1 điểm C trên AB với AC=a, BC=b. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn đường kính AB tại P. Dựng đường tròn tâm P bán kính r1, tiếp xúc với CA,CD và tiếp xúc với nửa đường tròn đường kính AB. Dựng đường tròn tâm Q bán kính r2 tiếp xúc với CB,CD và tiếp xúc với nửa đường tròn đường kính AB. Gọi r là bán kính đường tròn nội tiếp tam giác ABD
a/ Tính r1,r2 theo a,b
b/Tìm đẳng thức liên hệ giữa r,r1,r2
Tính bán kính của đường tròn tâm \(M( - 2;3)\) và tiếp xúc với đường thẳng \(d:14x - 5y + 60 = 0\).
Bán kính của đường tròn là:
\(R = d\left( {M,d} \right) = \frac{{\left| {14.( - 2) - 5.3 + 60} \right|}}{{\sqrt {{{14}^2} + {{\left( { - 5} \right)}^2}} }} = \frac{{\sqrt {221} }}{{13}}\)
Vậy bán kính cần tìm là \(\frac{{\sqrt {221} }}{{13}}\)
Đúng 0
Bình luận (0)
Giúp mình với!!!
Cho nửa đường tròn tâm O đường kính AB=2R (R>9). Trên bán kính OA lấy hai điểm C và D sao cho AC=6; AD=9. Đường thẳng vuông góc với AB tại D cắt nửa đường tròn tại E. Điểm F thuộc nửa đường tròn sao cho ^ACF=^DCE. Đường tròn tâm I bán kính r tiếp xúc với 2 cạnh của góc ECF và tiếp xúc trong với đường tròn tâm O. Tính r.