Cho hình thang cân ABCD, đáy lớn CD, đáy nhỏ AB. CMR: có 1 đường tròn đi qua 4 đỉnh A,B,C,D
Cho hình thang cân ABCD, đáy lớn CD, đáy nhỏ AB. CMR: có 1 đường tròn đi qua 4 đỉnh A,B,C,D
AB // CD (gt) nên \(\widehat{A}+\widehat{D}=180^0\)
Mà \(\widehat{A}=\widehat{B}\Rightarrow\widehat{B}+\widehat{D}=180^0\)
Do đó: ABCD là tứ giác nội tiếp nên có 1 đường tròn đi qua cả 4 đỉnh A,B,C,D
Cho hình thang cân ABCD, đáy lớn CD, đáy nhỏ AB. CMR: có 1 đường tròn đi qua 4 đỉnh A,B,C,D
Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB. Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh D của nó.
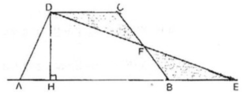
Dựa trên hình vẽ câu a ta chọn điểm K là trung điểm AE.
1. Cho hình thang ABCD (đáy nhỏ AB, đáy lớn CD). Qua A vẽ đường thẳng song song BC cắt đường chéo BD tại E. Qua B vẽ đường thẳng song song AD cắt đường chéo AC tại F.
a, CMR: DEFC là hình thang cân
b, Tính EF biết AB=5cm, CD=10cm.
1. Cho hình thang ABCD (đáy nhỏ AB, đáy lớn CD). Qua A vẽ đường thẳng song song BC cắt đường chéo BD tại E. Qua B vẽ đường thẳng song song AD cắt đường chéo AC tại F.
a, CMR: DEFC là hình thang cân
b, Tính EF biết AB=5cm, CD=10cm.
cho hình thang ABCD có đáy nhỏ là AB, đáy lớn là CD. CMR: góc A +góc B > góc C+góc D
Cho hình thang cân ABCD có đáy nhỏ AB=1, đáy lớn CD=3, cạnh bên A D = 2 quay quanh đường thẳng AB. Tính thể tích V của khối tròn xoay tạo thành.
![]()
![]()
![]()
![]()
Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB
a) Hãy vẽ tam giác ADE mà diện tích của nó bằng diện tích hình thang đã cho. Từ đó suy ra cách tính diện tích hình thang dựa vào độ dài hai cạnh đáy và độ dài đường cao của hình thang
b) Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh D của nó ?
Kéo dài AB về phía B một đoạn BE=DC. Nối DE cắt BC tại M.
Do CD // BE nên ta có tam giác MDC = tam giác MEB (trường hợp g.c.g). Suy ra dt(ABCD)=dt(ABMD) + dt(MDC) = dt(ABMD) + dt(MEB) = dt(DAE) = 1/2 .AE . h =1/2 (AB + BE).h = \(\dfrac{AB+CD}{2}.h\)
b) Theo câu a) thì diện tích hình thang ABCD bằng diện tích tam giác DAE nên ta nối D với trung điểm N của AE thì DN sẽ chia tam giác DAE thành 2 phần bằng nhau. Khi đó diện tích tam giác DAN bằng nửa diện tích hình thang ABCD.
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
Cho hình thang cân ABCD, đáy nhỏ AB=a, đáy lớn CD=4a, canh bên bằng\(\frac{5a}{2}\). Chứng minh rằng tồn tại đường tròn nội tiếp hình thang ABCD