Làm câu c thôi ạ
NT
Những câu hỏi liên quan
Câu d thôi ạ, câu a, b, c làm rồi ạ
Gấp ạ!!! Làm câu c thôi ạ
c: Ta có: AM//BC
AE⊥BC
Do đó:AM⊥AE
Suy ra: \(\widehat{AME}+\widehat{AEM}=90^0\)
hay \(\widehat{AME}+\widehat{BAD}=90^0\)
Đúng 0
Bình luận (0)
Làm cho em bài 3 với ạ , làm giúp em câu C thôi ạ.Em cảm ơn ạ 
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
Đúng 0
Bình luận (0)
Làm giúp em câu C thôi ạ
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)
Đúng 0
Bình luận (0)

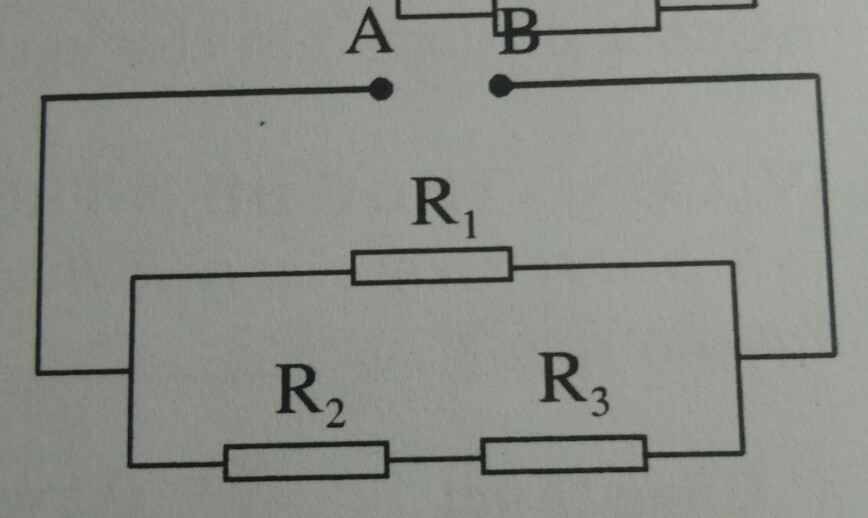
Làm giúp em câu C thôi ạ
\(a.R_{tđ}=\dfrac{R_1.\left(R_2+R_3\right)}{R_1+R_2+R_3}=\dfrac{6.\left(2+4\right)}{6+2+4}=3\Omega\\ b.U_{AB}=I.R_{tđ}=2.3=6V\\ c.Vì.R_1//R_{23}\Rightarrow U_{AB}=U_1=U_{23}=6V\\ I_1=\dfrac{U_1}{R_1}=\dfrac{6}{6}=1A\\ I_{23}=I-I_1=2-1=1A\\ Vì.R_2ntR_3\Rightarrow I_{23}=I_2=I_3=1A\)
Đúng 4
Bình luận (0)
 làm hộ câu b,c,d thôi ạ
làm hộ câu b,c,d thôi ạ
b: \(=\dfrac{x^2-x+1-3+1-x^2}{\left(x+1\right)\cdot\left(x^2-x+1\right)}=\dfrac{-x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{-1}{x^2-x+1}\)
Đúng 0
Bình luận (0)
Làm hộ em bài 11 Chỉ cần làm câu c d thôi ạ🥺
Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Đúng 3
Bình luận (1)

làm nhanh giúp mình câu b và c thôi ạ
Mn giúp em làm bài hình này câu c d thôi ạ đc không ạ?:)
E xin cảm ơn




