a, Diện tích tam giác ABC là :

          S ABC^2 = (4+5+8)/2 . [(4+5+8)/2-4] . [(4+5+8)/2-5] . [(4+5+8)/2-6] 

                        = 8,5 . 4,5 . 3,5 . 0,5 = 669,375 ( công thức hê-rông rùi bình phương 2 vế lên )

=> S ABC = 25,87228247 (cm²)

Tk mk nha

AM là trung tuyến của tam giác ABC cân tại A

=> AM là đường trung trực của tam giác ABC

=> M là trung điểm của BC

=> \(BM=CM=\frac{BC}{2}=\frac{32}{2}=16\) (cm)

Tam giác ABM vuông tại M có:

\(AB^2=AM^2+BM^2\)

\(34^2=AM^2+16^2\)

\(AM^2=34^2-16^2\)

\(AM^2=1156-256\)

\(AM^2=900\)

\(AM=\sqrt{900}\)

\(AM=30\) (cm)

Chúc bạn học tốt

Tớ làm thế này có đúng ko nhé

Vì đường trung tuyến đi qua trung điểm của

đoạn thẳng BC

   Suy ra: BM=CM=32:2=16cm

Xét tam giác ABM và AMC

  AB=AC(gt)

  AM là cạnh chung

  MB=MC(gt)

⇒tam giác ABM=tam giác AMC(c.c.c)

Do đó góc AMB=góc AMC(1)

Mà góc AMB+gócAMC=180(kề bù)(2)

Từ 1 và 2 suy ra góc AMB= góc AMC=90 độ

    Xét tam giác ABM vuông tại M

Áp dụng định lý Pi-Ta-Go ta có

 AM²+BM²=AB²

 AM²+16²=34²

 AM=34²-16²=900

 AM=30

vậy AM=30 cm

Xét tam giác ABM và tam giác ACM có:

              AB=AC      (GT)

         góc B= góc C          (GT) 

              BM=CM            (GT)

=> tam giác ABM= tam giác ACM (c.g.c)

=> góc AMB = góc AMC                ( 2 góc tương ứng)

Mà góc AMB + góc AMC = 180^o                 (2 góc kề bù)

=>góc AMB= góc AMC = 90^o

=> AM vuông góc với BC

Ta có: MB=MC=32/2=16   (cm)

Tam giác AMC vuông tại M

=>theo định lý Py-ta-go:

AM² = AC² – MC² = 900

⇒ AM = 30 (cm) 

 

tam giác ABC cân ở A 

tiếp tuyến AM

suy ra : AM vuông góc với BC 

mà M là trung điểm của BC (AM là tiếp tuyến) suy ra MB =16cm

áp dụng pytago vào tam giác AMB suy ra AM= 30cm

Xét tam giác ABM và tam giác ACM có:

              AB=AC      (GT)

         góc B= góc C          (GT) 

              BM=CM            (GT)

=> tam giác ABM= tam giác ACM (c.g.c)

=> góc AMB = góc AMC                ( 2 góc tương ứng)

Mà góc AMB + góc AMC = 180^o                 (2 góc kề bù)

=>góc AMB= góc AMC = 90^o

=> AM vuông góc với BC

Ta có: MB=MC=32/2=16   (cm)

Tam giác AMC vuông tại M

=>theo định lý Py-ta-go:

AM² = AC² – MC² = 900

⇒ AM = 30 (cm) 

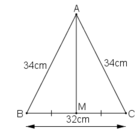
Do M là trung điểm của BC nên BM = CM = BC/2 cm

Tam giác AMB có ∠(AMB) = 90o

Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:

AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162

= 1156 - 256 = 900

Suy ra: AM = 30 (cm).

Ta có:AM là trung tuyến tam giác ABC

=> MB=MC=BC/2=32/2=16 (cm)

=> AM=MB=MC=16 cm ( gt)

Vì đường trung tuyến đi qua trung điểm của

đoạn thẳng BC

   Suy ra: BM=CM=32:2=16cm

Xét tam giác ABM và AMC

  AB=AC(gt)

  AM là cạnh chung

  MB=MC(gt)

\(\Rightarrow\)tam giác ABM=tam giác AMC(c.c.c)

Do đó góc AMB=góc AMC(1)

Mà góc AMB+gócAMC=180(kề bù)(2)

Từ 1 và 2 suy ra góc AMB= góc AMC=90 độ

    Xét tam giác ABM vuông tại M

Áp dụng định lý Pi-Ta-Go ta có

 AM²+BM²=AB²

 AM²+16²=34²

 AM=34²-16²=900

 AM=30

vậy AM=30 cm

đúng không bạn gì ơi

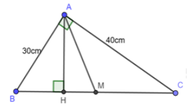
Áp dụng định lý Pytago cho  ABH vuông tại A có:

Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:

Vì AM là đường trung tuyến  M là trung điểm BC

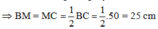
Ta có: MH = BM – BH = 25 – 18 = 7 cm

Đáp án cần chọn là: A

Áp dụng định lý Py-ta-go, ta có:

\(BC^2=AB^2+AC^2\)

\(BC^2=6^2+8^2=100=10\left(cm\right)\)

Ta lại có, đường trung tuyến ứng với cạnh huyền thì bằng một nửa cạnh huyền

\(\Rightarrow AM=10:2=5\left(cm\right)\)