a: Xét ΔADB và ΔAEC có

góc A chung

AB=AC
góc ABD=góc ACE

=>ΔADB=ΔAEC

=>AD=AE

b: Xét ΔABC có AE/AB=AD/AC

nên ED//BC

ED//BC

=>góc EDB=góc DBC

=>góc EDB=góc EBD

=>ED=EB

Xét tứ giác BEDC có

DE//BC

BD=CE

=>BEDC là hình thang cân

=>EB=DC=ED

c: Xét ΔOBC có góc OBC=góc OCB

nên ΔOBC cân tại O

=>OB=OC

OB+OD=BD

OC+OE=CE
mà OB=OC và BD=CE

nên OD=OE

=>ΔODE cân tạiO

a)vì góc B=góc C

mà góc IBC=1/2 góc EBC và ICB=1/2 góc DCB

nên suy ra IBC=ICB suy ra IBC là tam giác cân

b)xét tam giác ECB và tam giác DBC có

BC là cạnh chung

góc ECB= góc DBC(câu a)

góc B= góc C

suy ra tam giác ECB = tam giác DBC (g.c,g)

cho cái k xong sẽ làm câu c và d

làm đi  -_-  cho rồi đó

cần gấp!!!

lâu thế!!

Gọi giao điểm của BE và CD là I.

Xét tam giác ABC cân tại A nên \(\widehat{B}=\widehat{C}\)

Tia phân giác của \(\widehat{B}\)và \(\widehat{C}\)cắt lần lượt tại D và E nên:

\(\widehat{ICB}=\widehat{IBC}\) và ID=IE

Vậy tam giác IBC cân và IB=IC.

Xét tam giác IBD và tam giác IEC có:

\(\widehat{EIC}=\widehat{DIB}\)(đối đỉnh)

IB=IC(cmt)

ID=IE(cmt)

Suy ra \(\Delta IDB=\Delta EIC\)(c.g.c)

=>BD=CE(2 cạnh tương ứng)

+) Xét \(\Delta\)ABC cân tại A

\(\Rightarrow\) AB = AC  ( tính chất tam giác cân )

và \(\widehat{ABC}=\widehat{ACB}\)

\(\Rightarrow\frac{\widehat{ABC}}{2}=\frac{\widehat{ACB}}{2}\)

\(\Rightarrow\widehat{B_1}=\widehat{C_2}\)

+) Xét \(\Delta\) ABD và \(\Delta\) ACE có

\(\widehat{B_1}=\widehat{C_2}\)   ( cmt)

AB = AC  ( cmt)

\(\widehat{A}\) : góc chung

=> \(\Delta\)ABD = \(\Delta\) ACE  (g-c-g)

=> BD = CE  ( 2 cạnh tương ứng )

@@ Học tốt

Takigawa Miu_

Ta có : Góc B = Góc C

=>B/2=C/2

=>DBC^=ECB^

Xét Tam giác ECB và Tam giác DBC

BC cạnh chung

DBC^=ECB^ (cmt)

B^=C^(gt)

=>Tam giác ECB=tam giác DBC (g-c-g)

=>BD=CE (2 cạnh tương ứng)

=>ĐPCM

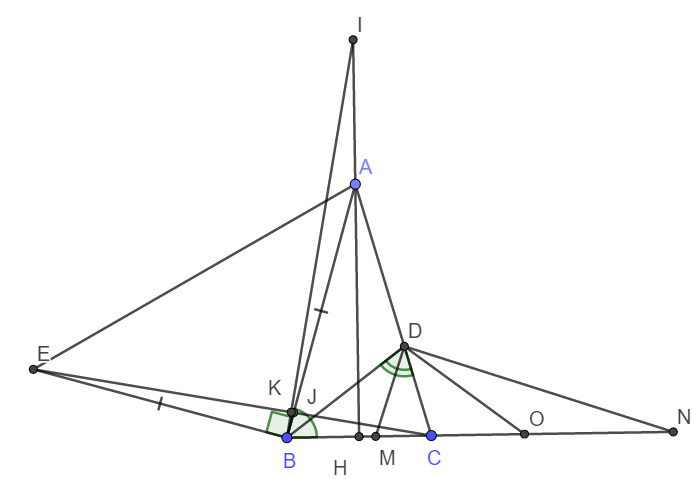
a)

+) Do tam giác ABC cân tại A nên trung tuyến AH đồng thời là đường caio.

Vậy nên \(\widehat{AHB}=90^o\)

Theo tính chất góc ngoài của tam giác, ta có:

\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)

Xét tam giác ABI và tam giác BEC có:

AI = BC (gt)

BA = EB (gt)

\(\widehat{IAB}=\widehat{CBE}\)  (cmt)

\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)

+) Gọi giao điểm của EC với AB và BI lần lượt là J và K.

Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)

Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)

Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)

b) Gọi O là trung điểm MN. Ta thấy DN và DM là phân giác của hai góc kề bù nên chúng vuông góc với nhau.

Vậy tam giác DMN vuông tại D. Khi đó ta có DO là trung tuyến ứng với cạnh huyền nên DO  =  MN/2

Vậy DO = OM = OM hay các tam giác DOM và DON cân tại O.

Ta có: \(\widehat{DOM}=180^o-2\widehat{DMO}=180^o-2\left(\widehat{MDB}+\widehat{MBD}\right)\)

\(=180^o-2.\widehat{MDB}-2.\widehat{MBD}=180^o-\widehat{BDC}-\widehat{ABC}\)

\(=180^o-\widehat{BDC}-\widehat{ACB}=\widehat{DBO}\)

Vậy tam giác DBO cân tại D hay DB = DO.

Vậy nên BD = MN/2.

xét tam giác BAI va CBE

be=ab

bc=ia

iab=ebc

=>tam giác BAI=tam giác CBE

2222222🐥

Em tham khảo tại đây nhé.

Câu hỏi của Nguyễn Minh Huy - Toán lớp 7 - Học toán với OnlineMath