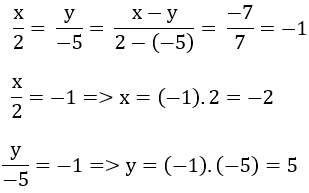So sánh:\(x^2\)\(và\)\(x\)\(biết:x\inℚ\)
BD
Những câu hỏi liên quan
a) Cho \(a^m=a^n\left(a\inℚ;m,n\inℕ\right)\). Tìm các số m và n
b) Cho \(a^m>a^n\left(a\inℚ;a>0;m,n\inℕ\right)\). So sánh m và n
a, \(a\in\left\{0,1\right\}\)
b, \(m>n\)
Đúng 0
Bình luận (0)
Tìm 2 số x và y,biết:x:2=y:(-5) và x-y=-7
Cho hàm số yfleft(xright)xác đinh với mọi xinℚvà có tính chất fleft(x_1cdot x_2right)x_1cdot fleft(x_2right)với mọi x_1và x_2inℚ. CMR: Nếu f(1)a (ane0) thì yf(x)ax với mọi xinℚ
Đọc tiếp
Cho hàm số \(y=f\left(x\right)\)xác đinh với mọi \(x\inℚ\)và có tính chất \(f\left(x_1\cdot x_2\right)=x_1\cdot f\left(x_2\right)\)với mọi \(x_1\)và \(x_2\)\(\inℚ\). CMR: Nếu f(1)=a (a\(\ne\)0) thì y=f(x)=ax với mọi x\(\inℚ\)
tìm 2 số x và y biết:x/2=y/3 và x+y=20 ?
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
\(\frac{x}{2}=\frac{y}{3}=\frac{x+y}{2+3}=\frac{20}{5}=4\)
Suy ra: \(\frac{x}{2}=4\Rightarrow x=4\cdot2=8\)
\(\frac{y}{3}=4\Rightarrow y=3\cdot4=12\)
Đúng 0
Bình luận (0)
Tìm x,y biết:x/5=y/4 và x^2-y^2=1
dat \(\frac{x}{5}=\frac{y}{4}=k\)-> x=5k va y=4.k
thay x=5k va y=4k vao x2-y2=1 ta duoc
(5k)2-(4k)2=1
25k2-16k2=1
9k2=1
k2=\(\frac{1}{9}=\left(\frac{1}{3}\right)^2\)
-> k=1/3 hay k=-1/3
voi K=1/3--> x=5.1/3=5/3 va y=4.1/3=4/3
voi K=-1/3->x=5.-1/3=-5/3 va y=4.-1/3=-4/3
Đúng 0
Bình luận (0)
Tìm hai số x,y biết:
x : 1,2 = y : 0,4 và x – y = 2.
Vì x : 1,2 = y : 0,4 nên \(\frac{x}{{1,2}} = \frac{y}{{0,4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{1,2}} = \frac{y}{{0,4}} = \frac{{x - y}}{{1,2 - 0,4}} = \frac{2}{{0,8}} = 2,5\)
Vậy x = 1,2 . 2,5 = 3; y = 0,4 . 2,5 = 1
Đúng 0
Bình luận (0)
tìm hai số x,y biết:x/5 =y/3 và x-y=-2
Ta có : `x/5=y/3` và `x-y=-2`
ADTC dãy tỉ số bằng nhau ta có :
`x/5 = y/3 =(x-y)/(5-3)=(-2)/2=-1`
`=>x/5=-1=>x=-1.5=-5`
`=>y/3=-1=>y=-1.3=-3`
Vậy `x=-5;y=-3`
Đúng 3
Bình luận (0)
Áp dụng tính chất của DTSBN, ta được:
x/5=y/3=(x-y)/(5-3)=-2/2=-1
=>x=-5; y=-3
Đúng 0
Bình luận (0)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x-y}{5-3}=\dfrac{-2}{2}=-1\)
Suy ra \(\dfrac{x}{5}=-1=>x=-1.5=>x=-5\)
\(\dfrac{y}{3}=-1=>y=-1.3=-3\)
Vậy x=-5; y=-3
Đúng 1
Bình luận (0)
Tìm x \(\inℚ\)
| x + 2 | + | x - 2 | = 4
ta xét 3 TH
TH1 x < -2
=> x+2 < 0 và x-2 < 0
=> | x + 2 | + | x - 2 | = -x - 2 + 2 - x = -2x = 4 => x = 2 (loại)
TH2 -2 < x < 2
=> x + 2 > 0 và x - 2 < 0
=> | x + 2 | + | x - 2 | = x + 2 + 2 -x = 4 = 4
TH2 này là TH đặc biệt nên mọi x \(\in\)Q mà -2<x<2 đều thỏa mãn (1)
TH3 x > 2
=> x + 2 > 0 và x - 2 < 0
=> | x + 2 | + | x - 2 | = x + 2 + x - 2 = 2x = 4 => x = 2 (t/m) (2)
kết hợp giữa 1 và 2 ta có với mọi x mà -2 < x < 2 \(x\in Q\)thì đều thỏa mãn
Đúng 0
Bình luận (0)
Tìm x,y,z biết:x/y=2và1/2 và x+y=63
\(\frac{x}{y}=\frac{21}{2}\Rightarrow\frac{x}{21}=\frac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{12}=\frac{y}{2}=\frac{x+y}{12+2}=\frac{63}{14}=4.5\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=4.5\rightarrow x=4.5\cdot12=54\\\frac{y}{2}=4.5\rightarrow y=4.5\cdot2=9\end{cases}}\)
Đúng 0
Bình luận (0)
\(\frac{x}{y}=\frac{21}{2}\)
\(\frac{x}{21}=\frac{y}{2}\)
Ta có
\(\frac{x}{12}=\frac{y}{2}=\frac{x+y}{12+2}=\frac{63}{14}=4.5\)
Đến đây ta chia 2 trường hợp rồi bn tự kết luận nhé !!!
Đúng 0
Bình luận (0)