
dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )
7) \(x+4\sqrt{x}+4=\left(\sqrt{x}\right)^2+2\sqrt{x}.2+2^2=\left(\sqrt{x}+2\right)^2\)
8) \(\left(\sqrt{x}-3\right)^2=\left(\sqrt{x}\right)^2-2.\sqrt{x}.3+3^2=x-6\sqrt{x}+9\)
9) \(x\sqrt{x}+y\sqrt{y}=\sqrt{x^3}+\sqrt{y^3}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)
10) \(x\sqrt{x}-y\sqrt{y}=\sqrt{x^3}-\sqrt{y^3}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\)
11) \(x\sqrt{x}+1=\sqrt{x^3}+1^3=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
12) \(x\sqrt{x}-8=\sqrt{x^3}-2^3=\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)\)
7. x + \(4\sqrt{x}+4\)
= \(\left(\sqrt{x}\right)^2+2.2.\sqrt{x}+2^2\)
= \(\left(\sqrt{x}+2\right)^2\)

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )
9) \(x-1=\left(\sqrt{x}\right)^2-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
10) \(x\sqrt{x}-1=\sqrt{x^3}-1=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
11) \(x-2\sqrt{x}-63=\left(x-2\sqrt{x}+1\right)-64=\left(\sqrt{x}-1\right)^2-8^2=\left(\sqrt{x}-1-8\right)\left(\sqrt{x}-1+8\right)=\left(\sqrt{x}-9\right)\left(\sqrt{x}+7\right)\)

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )
(a+b)^3 - (a-b)^3
các bạn giải chi tiết ra giúp mik vs nhé! mik đang cần gấp lắm!
ĐỀ BÀI LÀ: phân tích các đa thức sau thành nhân tử bằng phg pháp dùng hằng đẳng thức
(a+b)3-(a-b)3=a3+3a2b+3ab2+b3-(a3-3a2b+3ab2-b3)
=a3+3a2b+3ab2+b3-a3+3a2b-3ab2+b3
=6a2b+2b3
Áp dụng hđt a3-b3=(a-b)(a2+ab+b2) ấy
\(\left(a+b\right)^3-\left(a-b\right)^3=\left[\left(a+b\right)-\left(a-b\right)\right]\left[\left(a+b\right)^2+\left(a+b\right)\left(a-b\right)+\left(a-b\right)^2\right]\)
\(=\left(a+b-a+b\right)\left(a^2+2ab+b^2+a^2-b^2+a^2-2ab+b^2\right)\)
\(=2b\left(3a^2+b^2\right)\)
Ta có : \(\left(a+b\right)^3-\left(a-b\right)^3\)
\(=a^3+3a^2b+3ab^2+b^3-\left(a^3-3a^2b+3ab^2-b^3\right)\)
\(=a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3\)
\(=6a^2b+2b^3\)
RÚT GỌN CÁC BIỂU THỨC SAU:
Gợi ý: Dùng hằng đẳng thức để rút gọn nhanh hơn (nhưng cũng phải biến đổi rõ ràng ra rồi mới ra hằng đẳng thức chứ ko đc làm nhanh bằng cách ghi hằng đẳng thức ngay!)
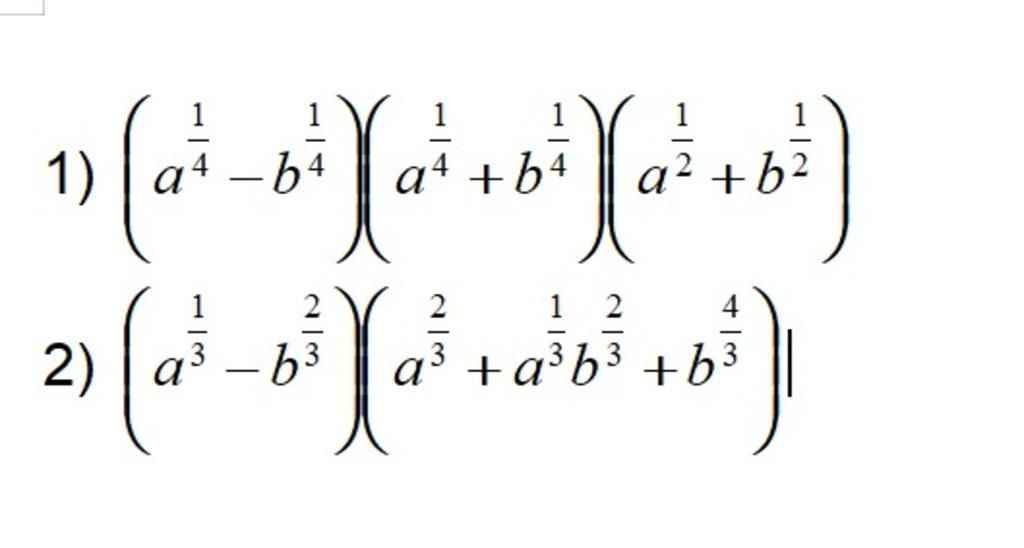
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
phân tích đa thức thành nhân tử 25-m2
gợi ý : dùng phương pháp hằng đẳng thức
giải chi tiết hộ với em mới học
\(\left(25-m^2\right)=\left(5-m\right)\left(5+m\right)\)
giải chi tiết hộ với em mới học
`25-m^2`
`=5^2-m^2`
`=(5-m)(5+m)`
Áp dụng HĐT : `a^2-b^2=(a-b)(a+b)`
phân tích đa thức thành nhân tử:
10a-25-a2
gợi ý : dùng phương pháp hằng đẳng thức
giải chi tiết hộ với em mới học
\(10a-25-a^2=-\left(a^2-10a+25\right)=-\left(a^2-2.a.5+5^2\right)=-\left(a-5\right)^2\)
`10a-25-a^2`
`=-(a^2-10a+25)`
`=-(a^2-2.a.5+5^2)`
`=-(a-5)^2`
Áp dụng hằng đẳng thức : `(a-b)^2=a^2-2ab+b^2`
-a ^2 + 10 a - 25
- ( a^2 -10 a + 25 )
- ( a - 5 )^2