xác định ab để:
M=(x+a)(x2-2n+b)
N=(x3+8)
H24
Những câu hỏi liên quan
xác định ab để:
M=(x+a)(x2-2n+b)
N=(x3+8) có gí trị bằng nhau
Ta có : \(N=x^3+8=\left(x+2\right)\left(x^2-2n+4\right)\)
Mà N = M => \(\left(x+2\right)\left(x^2-2n+4\right)=\left(x+a\right)\left(x^2-2n+b\right)\)
=> a = 2 , b = 4
...Good luck...!
Đúng 0
Bình luận (0)
Xác định tham số m để hàm số sau:
a)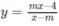 
đồng biến trên từng khoảng xác định;
b) y = − x 3 + m x 2 − 3x + 4 nghịch biến trên.
a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng ( - ∞ ; m), (m; + ∞ ) khi và chỉ khi:
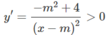
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Cho 2 đa thức :
N (x) = x2 + 3x4 - 2x - x2 + 2x3
P (x) = -8 + 5x - 6x3 - 4x + 6
A) rút gọn đa thức N (x) , P (x) và xác định bậc của chúng
B) Tính N(x) + P(x)
C) Tính B(x) = -2x2 ( x3 - 2x + 5x2 -1 )
\(a,N\left(x\right)=x^2+3x^4-2x-x^2+2x^3=3x^4+2x^3+\left(x^2-x^2\right)-2x\\ =3x^4+2x^3-2x\\ P\left(x\right)=-8+5x-6x^3-4x+6=-6x^3+\left(5x-4x\right)+\left(-8+6\right)\\ =-6x^3+x-2\)
Bậc của N(x) là 4
Bậc của P(x) là 3
\(b,P\left(x\right)+N\left(x\right)=3x^4+2x^3-2x-6x^3+x-2\\ =3x^4+\left(2x^3-6x^3\right)+\left(-2x+x\right)-2\\ =3x^4-4x^3-x-2\)
\(c,B\left(x\right)=-2x^2\left(x^3-2x+5x^2-1\right)\\ =\left(-2x^2\right).x^3+\left(-2x^2\right).\left(-2x\right)+\left(-2x^2\right).5x^2+\left(-2x^2\right).\left(-1\right)\\ =-2x^5+4x^3-10x^4+2x^2\\ =-2x^5-10x^4+4x^3+2x^2\)
Đúng 2
Bình luận (0)
xác định a,b để đa thức f(x) =x3 +ax+b chia hết cho x2 +x-6
Phân tích đa thức x2+ x-6 = (x-2)(x+3)
Gọi thương của phép chia f(x) cho đa thức trên là Q(x)
Ta có f(2)= 8+ 2a+b=0
Suy ra 2a+b=-8
lại có f(-3)= -27+ 3a+b=0
Suy ra 3a+b=27
đến đây ta dùng máy tính giải hệ ta được a=35;b=-78
Đúng 0
Bình luận (0)
H24
31 tháng 5 2021 lúc 15:56
Xác định a để đa thức: x3 + x2 + a – x \(⋮\) (x + 1)2
x³ +x² +a -x chia hết cho (x+1)²
Vậy x³ +x² +a -x = (x-1)(x+1)² +a +1
Để x³ +x² +a -x chia hết cho (x+1)² thì a+1 =0; mọi a
⇒ a = -1
Vậy a=-1 thì x³ +x² +a -x chia hết cho (x+1)²
Đúng 1
Bình luận (0)
H24
31 tháng 5 2021 lúc 16:20
Xác định a để đa thức: x3 + x2 + a – x \(⋮\) (x + 1)2.
Thực hiện phép chia đa thức \(x^3+x^2+a-x\) cho đa thức \(\left(x+1\right)^2\) ta được số dư là a + 1
=> Để: x3 + x2 + a – x ⋮ (x + 1)2 thì a + 1 = 0 => a = -1
Đúng 1
Bình luận (0)
Cho hàm số:
y = x3 + (m + 3)x2 + 1 - m (m là tham số)
có đồ thị (Cm).
a) Xác định m để hàm số có điểm cực đại là x = -1.
b) Xác định m để đồ thị (Cm) cắt trục hoành tại x = -2
Xác định giá trị của tham số m để hàm số
y = x 3 - 3(m - 1) x 2 - 3(m + 1)x - 5 có cực trị
A. m > 0 B. -1 < m < 1
C. m ≤ 0 D. ∀m ∈ R.
Đáp án: D.
y' = 3 x 2 - 6(m - 1)x - 3(m + 1)
y' = 0 ⇔ x 2 - 2(m - 1)x - m - 1 = 0
Δ' = ( m - 1 ) 2 + m + 1 = m 2 - m + 2 ≥ 0
Tam thức m 2 - m + 2 luôn dương với mọi m ∈ R vì δ = 1 - 8 < 0 và a = 1 > 0 cho nên phương y' = 0 luôn có hai nghiệm phân biệt. Suy ra hàm số luôn có cực trị với mọi giá trị m ∈ R.
Đúng 0
Bình luận (0)