gpt
(2x2 - x -1)2 -3 = 4x2 - 2x +2
`4x=2+xx+1x<=>4x=2+3x<=>4x-3x=2<=>1x=2<=>x=2`
1:áp dụng quy tắc đối đầu hay thực hiện phép tính cộng
2x+1/2x2-x + 32x2/1-4x2 +1-2x/2x2+x
2:tính
a,4x2/x-2 +3/x-2 +19/2-x
b,2x/x2+2xy +y/xy-2y2 +4/x2-4y2
Bài 2:
a: \(=\dfrac{4x^2+3-19}{x-2}=\dfrac{4x^2-16}{x-2}=\dfrac{4\left(x-2\right)\left(x+2\right)}{x-2}=4x+8\)
b: \(=\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2}{x+2y}-\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2x-4y-x-2y+4}{\left(x+2y\right)\left(x-2y\right)}\)
\(=\dfrac{x-6y+4}{\left(x+2y\right)\left(x-2y\right)}\)
Tìm x
a) ( 2x + 1 )2- 4x2 + 2x2 - 2 = 0
b) ( x - 2 ) . ( x + 2 ) - ( x + 3 )2 - 2x - 5 = 0
Giúp mình với ;-;
a. (2x + 1)2 - 4x2 + 2x2 - 2 = 0
<=> (2x + 1 - 2x)(2x + 1 + 2x) + 2(x2 - 1) = 0
<=> (4x + 1) + 2x2 - 2 = 0
<=> 4x + 1 + 2x2 - 2 = 0
<=> 2x2 + 4x - 2 + 1 = 0
<=> 2x2 + 4x - 1 = 0
<=> 2x2 + 4x = 1
<=> 2x(x + 2) = 1
Vì 1 chỉ có tích là 1 . 1 nên:
<=> \(\left[{}\begin{matrix}2x=1\\x+2=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
\(a,\Leftrightarrow4x^2+4x+1-4x^2+2x^2-2=0\\ \Leftrightarrow2x^2+4x-1=0\\ \Leftrightarrow2\left(x^2+2x+1\right)-3=0\\ \Leftrightarrow2\left(x+1\right)^2-3=0\\ \Leftrightarrow\left(x+1\right)^2=\dfrac{3}{2}\\ \Leftrightarrow\left[{}\begin{matrix}x+1=\sqrt{\dfrac{3}{2}}\\x+1=-\sqrt{\dfrac{3}{2}}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-\sqrt{6}}{2}\\x=\dfrac{-2+\sqrt{6}}{2}\end{matrix}\right.\)
\(b,\left(x-2\right)\left(x+2\right)-\left(x+3\right)^2-2x-5=0\\ \Leftrightarrow x^2-4-x^2-6x-9-2x-5=0\\ \Leftrightarrow-8x=18\\ \Leftrightarrow x=-\dfrac{9}{4}\)
Giải phương trình :
a ) ( 2 x – 1 ) ( 4 x 2 + 2 x + 1 ) – 4 x ( 2 x 2 – 3 ) = 23
b ) x + 2 x + 1 - 1 x - 2 = 1 - 3 x 2 - x - 2
a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
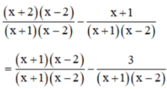
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.
1:áp dụng quy tắc đối đầu hay thực hiện phép tính cộng
2x+1/2x2-x + 32x2/1-4x2 +1-2x/2x2+x
2:tính
a,4x2/x-2 +3/x-2 +19/2-x
b,2x/x2+2xy +y/xy-2y2 +4/x2-4y2
Tìm x:
a, x(2x – 3) – 2(3 – 2x) = 0
b, (x – 3)(x2 + 3x + 9) – x(x + 2)(x – 2) = 1
c, 4x2 + 4x – 6 = 2
d, 2x2 + 7x + 3 = 0
\(a,\Leftrightarrow\left(2x-3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow x^3-27-x^3+4x=1\\ \Leftrightarrow4x=28\Leftrightarrow x=7\\ c,\Leftrightarrow4x^2-4x-8=0\\ \Leftrightarrow x^2-x-2=0\\ \Leftrightarrow\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ d,\Leftrightarrow2x^2+6x+x+3=0\\ \Leftrightarrow\left(x+3\right)\left(2x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Bài 5: Tìm nghiệm của các đa thức sau: Dạng 1: a) 4x + 9 b) -5x + 6 c) 7 – 2x d) 2x + 5 Dạng 2: a) ( x+ 5 ) ( x – 3) b) ( 2x – 6) ( x – 3) c) ( x – 2) ( 4x + 10 ) Dạng 3: a) x2 -2x b) x2 – 3x c) 3x2 – 4x d) ( 2x- 1)2 Dạng 4: a) x2 – 1 b) x2 – 9 c)– x 2 + 25 d) x2 - 2 e) 4x2 + 5 f) –x 2 – 16 g) - 4x4 – 25 Dạng 5: a) 2x2 – 5x + 3 b) 4x2 + 6x – 1 c) 2x2 + x – 1 d) 3x2 + 2x – 1
Bài 1: Rút gọn
C) (x2 - 3) (x2 +3) - 5x2 (x + 1)2 - (x2 - 3x) ( x2 - 2x) + 4x (x + 2)2
D) -6x2 (x + 5)2 - ( x - 3)2 + (x2 - 2) (2x2 + 1) - 4x2 ( 3x - 4)2
A) -2x(3x+2)(3x-2)+5(x+2)2 - (x-1)(2x+1)(2x+1)
= -2x(9x2-4)+5(x2+4x+4) - (x-1)(4x2-1)
= -18x3+8x+5x2+20x+20-(4x3-x-4x2+1)
= -18x3+5x2+28x+20-4x3+x+4x2+1
= -22x3+9x2+29x+21
B) (7x-8)(7x+8)-10(2x+3)2+5x(3x-2)2-4x(x-5)2
= 49x2 - 64 -10(4x2+ 12x + 3) + 5x(9x2 - 12x +4) - 4x(x2 - 10x +25)
= 49x2 - 64 -40x2 - 120x - 30 + 45x3 - 60x2 - 20x - 4x3 + 40x2 -100x
= 41x3 -11x2 -240x -94
C) \(\left(x^2-3\right)\left(x^2+3\right)-5x^2\left(x+1\right)^2-\left(x^2-3x\right)\left(x^2-2x\right)+4x\left(x+2\right)^2\)
\(\left(x^4-9\right)-5x^2\left(x^2+2x+1\right)-\left(x^4-2x^3-3x^3+6x^2\right)+4x\left(x^2+4x+4\right)\)
\(x^4-9-5x^4-10x^3-5x^2-x^4+5x^3-6x^2+4x^3+16x^2+16x\)
\(-5x^4-x^3+5x^2+20x-9\)
D) \(-6x^2\left(x+5\right)^2-\left(x-3\right)^2+\left(x^2-2\right)\left(2x^2+1\right)-4x^2\left(3x-4\right)^2\)
\(-6x^2\left(x^2+10x+25\right)-\left(x^2-6x+9\right)+2x^4-3x^2-2-4x^2\left(9x^2-24x+16\right)\)
\(-6x^4-60x^3+150x^2-x^2+6x-9+2x^4-3x^2-2-36x^4+96x^3-64x^2\)
\(-40x^4+36x^3+82x^2+6x-11\)
a) 3xy.(2x2 – 3yz + x3)
c) (2x + 3)2 + (2x – 3)2 – (2x + 3)(4x – 6) + xy
d) d) (4x2 + 4x + 1) : (2x + 1)
\(a,=6x^3y-9xy^2z+3x^4y\\ c,=\left(2x+3-2x+3\right)^2+xy=81+xy\\ d,=\left(2x+1\right)^2:\left(2x+1\right)=2x+1\)
Giair phương trình
1) 2x2-3x-2=0 7) (2x2-3x-4)2=(x2-x)2
2) 4x2-7x-2=0 8) \(\dfrac{2}{x+1}-\dfrac{3}{x+2}=\dfrac{1}{3x+3}\)
3) 4x2+5x-6=0 9) \(\dfrac{x}{x-3}=\dfrac{1}{x+2}\)
4) 4x2+5x-9=0 10) \(\dfrac{4}{2x-3}-\dfrac{7}{3x-5}=0\)
5) 5x2-18x-8=0 11) \(\dfrac{7}{x+2}+\dfrac{2}{x+3}=\dfrac{1}{x^2+5x+6}\)
6) (3x2+2x+4)2=(x2-4)2 12) \(\dfrac{4}{x-2}+\dfrac{x}{x+1}=\dfrac{x^2-2}{x^2-x-2}\)
Giúp em vs em đag cần câu tl gấp![]() em c.ơn trước
em c.ơn trước
giải phương trình làm dell gì, lớp 8 mà